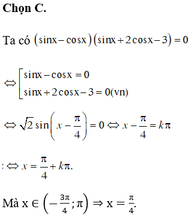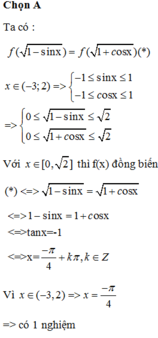Phương trình cosx=3/5 có tất cả bao nhiêu nghiệm trên khoảng (0;4pi)
LC
Những câu hỏi liên quan
Phương trình (sinx - cosx)(sinx + 2cosx - 3) 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng
-
3
π
4
;
π
? A. 3 B. 0. C. 1. D. 2.
Đọc tiếp
Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng - 3 π 4 ; π ?
A. 3
B. 0.
C. 1.
D. 2.
Cho hàm số
y
f
x
liên tục trên
ℝ
và có đồ thị như hình vẽ. Hỏi phương trình
f
1
-
sin
x
f
1
+
cos
x
có tất cả bao nhiêu nghiệm thuộc khoảng (-3;2). A.1 B.2 C.3 D.Vô số
Đọc tiếp
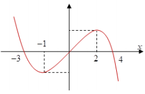
Cho hàm số y = f x liên tục trên ℝ và có đồ thị như hình vẽ. Hỏi phương trình
f 1 - sin x = f 1 + cos x có tất cả bao nhiêu nghiệm thuộc khoảng (-3;2).
A.1
B.2
C.3
D.Vô số
Phương trình sin x + cos x = 1 có bao nhiêu nghiệm trên khoảng 0 ; π .
A. 1
B. 0
C. 2
D. 3
1. Tìm tham số m để phương trình 3cos2x-7=2m có nghiệm?
2. Trên đoạn \([0;2\pi]\) , phương trình \(2cos^2x-\sqrt{3}cosx=0\)có bao nhiêu nghiệm?
3. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y=\sqrt{2cosx-3m+14}\) xác định với mọi x thuộc R?
Help me!!!
1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
Đúng 1
Bình luận (0)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)
Đúng 1
Bình luận (0)
1. Các nghiệm của phương trình \(\sqrt{3}sin2x-cos2x-2=0\) là?
2. Hàm số \(y=2cos3x+3sin3x-2\) có tất cả bao nhiêu giá trị nguyên dương?
3. Tìm tham số m để phương trình \(msinx-cosx=\sqrt{5}\) có nghiệm
Giúp mk với ạ!
1, Phương trình tương đương
\(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
⇔ \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
⇔ \(2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k.2\pi\)
⇔ x = \(\dfrac{\pi}{3}+k.\pi\)
2, \(2cos3x+3sin3x-2\)
= \(\sqrt{13}\)\((\dfrac{2}{\sqrt{13}}cos3x+\dfrac{3}{\sqrt{13}}sin3x)\) - 2
Do \(\left(\dfrac{2}{\sqrt{13}}\right)^2+\left(\dfrac{3}{\sqrt{13}}\right)^2=1\) nên tồn tại 1 góc a sao cho \(\left\{{}\begin{matrix}sina=\dfrac{2}{\sqrt{13}}\\cosa=\dfrac{2}{\sqrt{13}}\end{matrix}\right.\)
BT = \(\sqrt{13}sin\left(x+a\right)-2\)
Do - 1 ≤ sin (x + a) ≤ 1 với mọi x và a
⇒ \(-\sqrt{13}-2\le BT\le\sqrt{13}-2\)
⇒ \(-5,6< BT< 1,6\)
Vậy BT nhận 5 giá trị nguyên trong tập hợp S = {-5 ; -4 ; -3 ; -2 ; -1}
3. \(msinx-cosx=\sqrt{5}\)
⇔ \(\dfrac{m}{\sqrt{m^2+1}}.sinx-\dfrac{1}{\sqrt{m^2+1}}.cosx=\dfrac{\sqrt{5}}{\sqrt{m^2+1}}\)
⇔ sin(x - a) = \(\sqrt{\dfrac{5}{m^2+1}}\) với \(\left\{{}\begin{matrix}sina=\dfrac{1}{\sqrt{m^2+1}}\\cosa=\dfrac{m}{\sqrt{m^2+1}}\end{matrix}\right.\)
Điều kiện có nghiệm : \(\left|\sqrt{\dfrac{5}{m^2+1}}\right|\le1\)
⇔ m2 + 1 ≥ 5
⇔ m2 - 4 ≥ 0
⇔ \(\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Phương trình cos 2 x + cos x = 0 có bao nhiêu nghiệm thuộc khoảng − π ; π
A. 1
B. 4
C. 2
D. 3
Đáp án C.
Phương pháp
Sử dụng tính chất hai góc bù nhau cos x = cos π − x
Giải phương trình lượng giác cơ bản
Cách giải
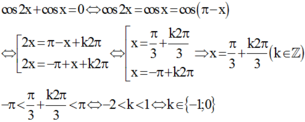
Vậy phương trình có 2 nghiệm thuộc − π ; π
Đúng 0
Bình luận (0)
Phương trình √3sinx - cosx = √2 có bao nhiêu nghiệm trên khoảng (-pi;pi)
Tính tổng hợp tất cả các nghiệm thuộc khoảng
0
;
π
của phương trình:
2
cos
3
x
sin
x
+
cos
x
A.
π
B.
3
π
C.
3
π
2
D.
π
2
Đọc tiếp
Tính tổng hợp tất cả các nghiệm thuộc khoảng 0 ; π của phương trình: 2 cos 3 x = sin x + cos x
A. π
B. 3 π
C. 3 π 2
D. π 2
Cho phương trình
1
+
cos
x
c
os
2
x
−
cos
x
−
sin
2
x
cos...
Đọc tiếp
Cho phương trình 1 + cos x c os 2 x − cos x − sin 2 x cos x + 1 = 0. Tính tổng tất cả các nghiệm năm trong khoảng 0 ; 2018 π của phương trình đã cho?
A. 1019090 π
B. 2037171 π
C. 2035153 π
D. 1017072 π
Đáp án D
ĐK: cos x ≠ − 1 . Khi đó P T ⇔ 1 + cos x 2 c os 2 x − cos x − 1 − 1 − c os 2 x 1 + cos x = 0
⇔ 2 c os 2 x − cos x − 1 − 1 − cos x = 0 ⇔ 2 c os 2 x = 2 ⇔ cos x = 1 cos x = − 1 ( l o a i ) ⇔ x = k 2 π
Do x ∈ 0 ; 2018 ⇒ k ∈ 1 ; 1008 ⇒ ∑ = 1 + 2 + 3 + ... + 1008 .2 π = 1 + 1008 2 .1008.2 π = 1017072 π
Đúng 0
Bình luận (0)