Tìm tập hợp tất cả các giá trị của m để đồ thị hàm số y = 2 x + m x + 1 cắt đường thẳng y=1-x tại hai điểm phân biệt
A. ( - ∞ ; 2 ]
B. ( - ∞ ; 2 )
C. ( - ∞ ; - 2 )
D. ( 2 ; + ∞ )
Cho hàm số y=f(x) có đồ thị như hình vẽ.
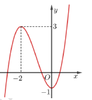
Tìm tập hợp tất cả các giá trị của m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
A. m < 2.
B. m > 2.
C. m > − 2.
D. m < − 2.
Đáp án D
Dựa vào đồ thị hàm số, dễ thấy hàm số f x = x 3 + 3 x 2 − 1
Xét hàm số f x + m = x + m 3 + 3 x + m − 1 với x ∈ ℝ
Chú ý : Cực trị là điểm làm y' đổi dấu và f x = x = x 2 ⇒ f ' x = 2 x 2 x 2 = x x
Do đó f x + m = 3 x + m x + m + 2 . x x .
Khi đó y = f x + m có 5 điểm cực trị x + m = 0 x + m + 2 = 0 có 4 nghiệm phân biệt x = − m x = − 2 − m có 4 nghiệm − m > 0 − 2 − m > 0 ⇔ m < − 2
Cách 2: Đồ thị hàm số y = f x + m được suy ra từ
y = f x → y = f x + m → y = f x + m .
Đồ thị hàm số muốn có 5 điểm cực trị khi ở bước thứ 1ta dịch chuyển đồ thị sang phải nhiều hơn 2 đơn vị m < − 2
Tìm tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y = 1 + x + 1 x 2 − m x − 3 m có đúng hai tiệm cận đứng ?
A. − ∞ ; − 12 ∪ 0 ; + ∞
B. 0 ; + ∞
C. 1 4 ; 1 2
D. 0 ; 1 2
Đáp án D
Đồ thị hàm số có 2 tiềm cận đứng
⇔ x ≥ − 1 x 2 − m x − 3 m = 0 có 2 nghiệm phân biệt.
⇔ x ≥ − 1 x 2 = m x + 3 ⇔ x ≥ − 1 m = x 2 x + 3 → f x = x 2 x + 3 có 2 nghiệm phân biệt
Xét hàm số f x = x 2 x + 3 trên − 1 ; + ∞ , có: f ' x = x x + 6 x + 3 2 ; f ' x = 0 ⇔ x = 0
Tính cách giác trị f − 1 = 1 2 ; f 0 = 0 và lim x → + ∞ f x = + ∞
Khi đó, yêu cầu * ⇔ m ∈ 0 ; 1 2 . Vậy m ∈ 0 ; 1 2 là giá trị cần tìm
Biết S = (a,b) là tập hợp tất cả các giá trị của tham số m để đường thẳng y = m cắt đồ thị hàm số y = | \(x^2-4x+3\) | tại bốn điểm phân biệt . Tìm a + b
Tập hợp tất cả các giá trị của tham số m để đường thẳng y = − 2 x + m tiếp xúc với đồ thị hàm số y = x + 1 x − 1 là
A. m ∈ 7 ; − 1 .
B. m = 6.
C. m ∈ 6 ; − 1 .
D. m = − 1.
Tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = − 2 x + m cắt đồ thị của hàm số y = x + 1 x − 2 tại hai điểm phân biệt là:
A. 5 − 2 3 ; 5 + 2 3
B. − ∞ ; 5 − 2 6 ∪ 5 + 2 6 ; + ∞
C. − ∞ ; 5 − 2 3 ∪ 5 + 2 3 ; + ∞
D. − ∞ ; 5 − 2 6 ∪ 5 + 2 6 ; + ∞
Tìm tập hợp tất cả các giá trị của tham số m để đường thẳng y=x+1 cắt đồ thị hàm số y = 2 x + m x - 1 tại hai điểm phân biệt có hoành độ dương
A. -2 < m < -1
B. m < -1
C. m < 1
D. -2 < m < 1
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
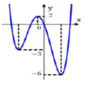
A. 9
B. 7
C. 12
D. 18
Hình vẽ bên là đồ thị của hàm số y=f(x). Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = f x − 1 + m có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
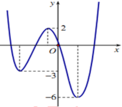
A. 12
B. 15
C. 18
D. 9
Tập hợp tất cả các giá trị của m để đồ thị hàm số y = 2017 + x + 1 x 2 − m x − 3 m có hai đường tiệm cận đứng là:
A. 1 4 ; 1 2
B. 0 ; 1 2
C. 0 ; + ∞
D. − ∞ ; − 12 ∪ 0 ; + ∞
Đáp án B
Để đồ thị hàm số có hai đường tiệm cận đứng ⇔ x 2 − m x − 3 m = 0 có hai nghiệm phân biệt x 1 , x 2 ≥ − 1.
⇔ Δ > 0 x 1 + x 2 ≥ − 2 x 1 + 1 x 2 + 1 ≥ 0 ⇔ Δ = − m 2 − 4 − 3 m > 0 x 1 + x 2 ≥ − 2 x 1 x 2 + x 1 + x 2 + 1 ≥ 0 ⇔ m 2 + 12 m > 0 m ≥ − 2 1 − 2 m ≥ 0 ⇔ m ∈ 0 ; 1 2 .