Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường y = 1 − x 2 , y = 0 quanh trục Ox có kết quả viết dưới dạng a π b (a, b nguyên tố cùng nhau). Khi đó a + b bằng
A. 11
B. 17
C. 31
D. 2
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y = x 4 , y = 0 , x = 1 , x = 4 khi quay quanh trục Ox bằng:
A. 7 36 π .
B. 1 12 π .
C. 2 π .
D. 21 16 π .
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y = x 4 , y = 0 , x = 1 , x = 4 khi quay quanh trục Ox bằng
A. 7 36 π
B. 1 12 π
C. 2 π
D. 21 16 π
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = x e x 2 , y = 0 , x = 0 , x = 1 xung quanh trục Ox là.
A. V = 9 π 4
B. V = π 2 e
C. V = π e - 2
D. V = e - 2
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = xe x , y=0, x=0, x=1 xung quanh trục Ox là:
A. 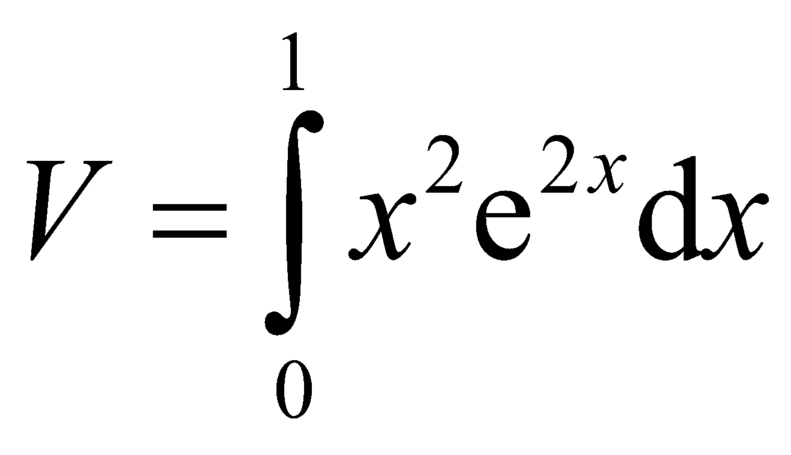
B. 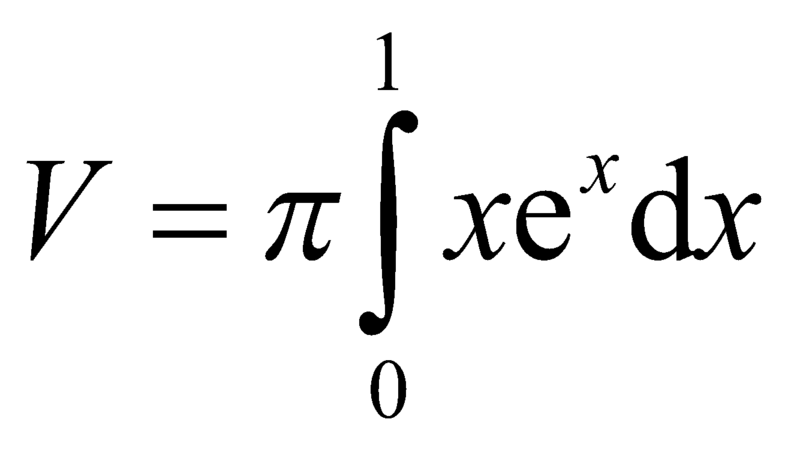
C. 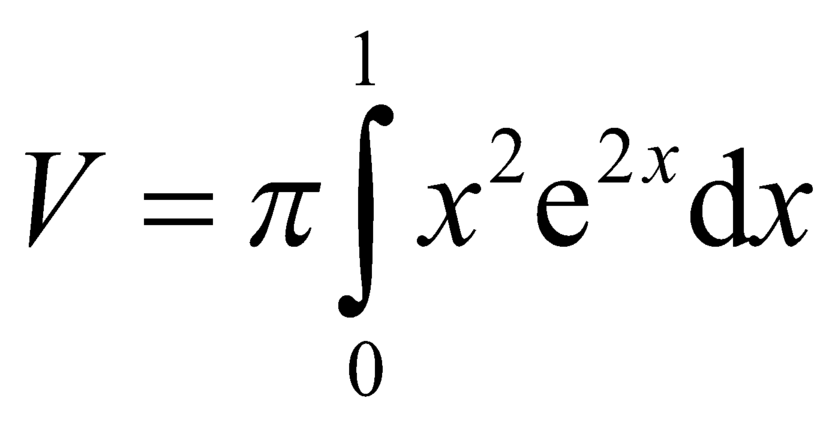
D. 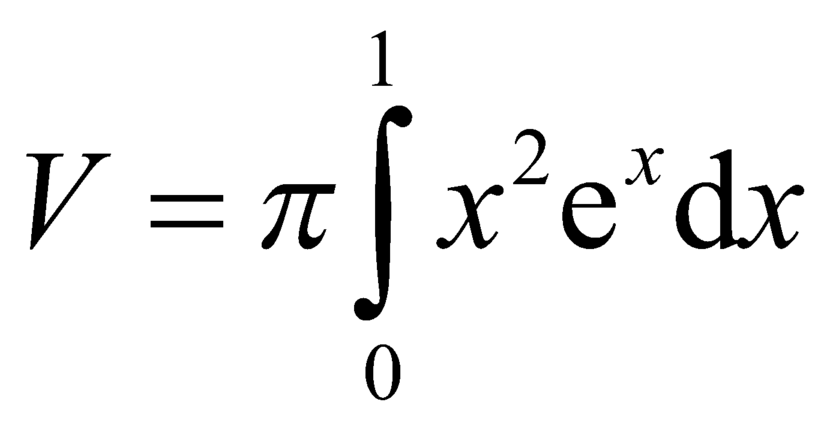
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y = x/4; y = 0; x = 1; x = 4 khi quay quanh trục Ox bằng:
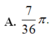
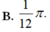
![]()
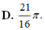
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường thẳng y = x e x , y = 0 , x = 0 , x = 1 xung quanh trục Ox là
A. V = ∫ 0 1 x 2 e 2 x d x
B. V = ∫ 0 1 x e x d x
C. V = π ∫ 0 1 x 2 e 2 x d x
D. V = π ∫ 0 1 x 2 e x d x
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường thẳng y = x e x ; y = 0; x = 1 xung quanh trục Ox là
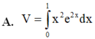
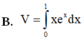
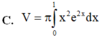
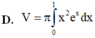
Áp dụng công thức ta có thể tích hình phẳng bài cho là:
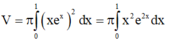
Đáp án C
Thể tích V của khối tròn xoay tạo thành khi quay quanh trục Ox hình phẳng giới hạn bởi các đường y = x 3 y = 0 , x = 1 , x = 8 .
A. π 3
B. 93 π 5
C. 9 π 4
D. 8 π
Đáp án B

Khi quay D quanh Ox tạo thành khối tròn xoay có thể tích là:
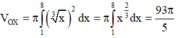
Thể tích V của khối tròn xoay tạo thành khi quay quanh trục Ox hình phẳng giới hạn bởi các đường y = x 3 , y = 0 , x = 1 , x = 8
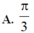
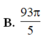
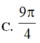
![]()
Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = tan x , y = 0 , x = 0 , x = π 4 xung quay trục Ox
A. V = π ln 2 4
B. V = ln 2
C. V = π 2 4
D. V = π ln 2
Đáp án D
V = π ∫ 0 π 4 tan x . d x = π ∫ 0 π 4 sin x cos x . d x = π ∫ π 4 0 d cos x cos x . d x = π . ln cos x 0 π 4 = − π . ln 1 2 = π . ln 2