Cho hàm số f x = x + 1 k h i x ≥ 0 e 2 x k h i x ≤ 0 . Tích phân I = ∫ − 1 2 f x d x có giá trị bằng bao nhiêu?
A. I = 7 e 2 + 1 2 e 2
B. I = 11 e 2 − 11 2 e 2
C. I = 3 e 2 − 1 e 2
D. I = 9 e 2 − 1 2 e 2
PB
Những câu hỏi liên quan
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Cho đồ thị của hàm số f’(x) trên khoảng K như sau:
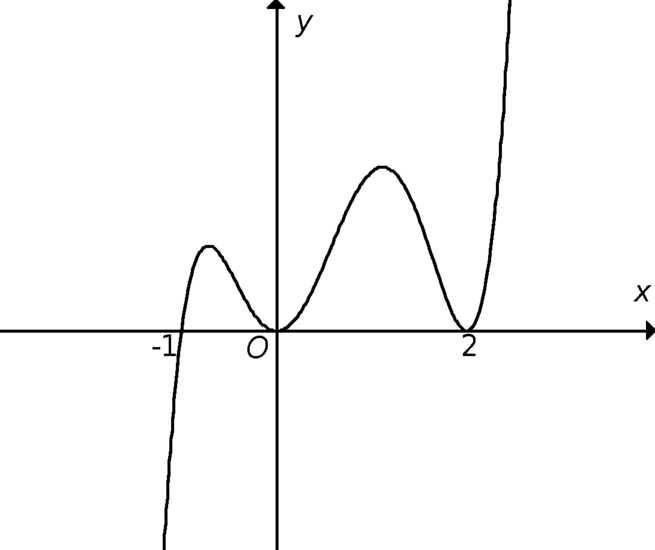
Số điểm cực trị của hàm số f(x) trên K là:
A. 1
B.2
C. 3
D. 4
Dựa vào đồ thị ta thấy phương trình 
chỉ có một nghiệm đơn và hai nghiệm kép nên 
chỉ đổi dấu khi qua nghiệm đơn này.
Do đó suy ra hàm số f(x) có đúng một cực trị.
Chọn A.
Đúng 0
Bình luận (0)
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Cho đồ thị của hàm số f’(x) trên khoảng K như sau: Số điểm cực trị của hàm số trên K là: A .1 B. 2 C. 3 D. 4
Đọc tiếp
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Cho đồ thị của hàm số f’(x) trên khoảng K như sau:
Số điểm cực trị của hàm số 
trên K là:
A .1
B. 2
C. 3
D. 4
Dựa vào đồ thị ta thấy phương trình 
có ba nghiệm đơn và 
đổi dấu khi qua nghiệm đơn này.
Do đó suy ra hàm số 
có ba điểm cực trị.
Chọn C.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định và liên tục trên khoảng K và có đạo hàm là f’(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f’(x) trên K. Sổ điểm cực trị của hàm số f(x) trên K là A. 2 B. 1 C. 3 D. 0
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên khoảng K và có đạo hàm là f’(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f’(x) trên K.
Sổ điểm cực trị của hàm số f(x) trên K là
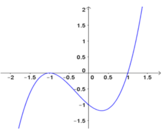
A. 2
B. 1
C. 3
D. 0
Đáp án B
Từ hình vẽ ta thấy, hàm số f'(x) = 0 có 2 nghiệm phân biệt x = 1 và x = -1.9x
Trong đó chỉ có tại x = 1 thì f'(x) đổi dấu từ âm sang dương, do đó hàm số y = f(x) có một điểm cực trị.
Đúng 0
Bình luận (0)
Hàm số y f( x) liên tục trên khoảng K, biết đồ thị của hàm số yf ’(x) trên K như hình vẽ. Tìm số cực trị của hàm số g(x) f(x+ 1) trên K? A.0. B. 1 C. 2. D. 3.
Đọc tiếp
Hàm số y= f( x) liên tục trên khoảng K, biết đồ thị của hàm số y=f ’(x) trên K như hình vẽ.
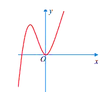
Tìm số cực trị của hàm số g(x) = f(x+ 1) trên K?
A.0.
B. 1
C. 2.
D. 3.
Chọn B
Để g( x) = f( x+ 1) => g’(x) = f’( x+1)
Hàm số y= g’(x) = f’( x+ 1) có đồ thị là phép tịnh tiến của đồ thị hàm số y= f’(x) theo phương trục hoành sang trái 1 đơn vị.
Khi đó đồ thị hàm số y= g’(x)= f’( x+1) vẫn cắt trục hoành tại 1 điểm.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
4
-
4
x
2
+
6
x
+
1
Hệ số góc k của tiếp tuyến của đồ thị hàm số f (x)...
Đọc tiếp
Cho hàm số f ( x ) = x 4 - 4 x 2 + 6 x + 1 Hệ số góc k của tiếp tuyến của đồ thị hàm số f '(x) tại điểm có hoành độ x = 1 là
A. k = -4
B. k = -8
C. k = 4
D. k = 20
Cho hàm số
y
f
x
xác định và liên tục trên khoảng K và có đạo hàm là f’(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f’(x) trên K.Sổ điểm cực trị của hàm số f(x) trên K là A. 2 B. 1 C. 3 D. 0
Đọc tiếp
Cho hàm số y = f x xác định và liên tục trên khoảng K và có đạo hàm là f’(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f’(x) trên K.
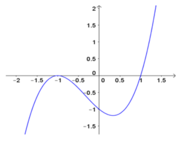
Sổ điểm cực trị của hàm số f(x) trên K là
A. 2
B. 1
C. 3
D. 0
Đáp án B
Từ hình vẽ ta thấy, hàm số f'(x) = 0 có 2 nghiệm phân biệt x = 1 và x = -1.
Trong đó chỉ có tại x = 1 thì f'(x) đổi dấu từ âm sang dương, do đó hàm số y = f(x) có một điểm cực trị.
Đúng 0
Bình luận (0)
Cho hàm số y=f(x)=x; y=g(x)=-2x; y=h(x)=1; y=k(x)=5; y=z(x)=\(\frac{1}{x}\); y=t(x)=\(^{x^2}\). Trong các hàm số trên, hàm số nào có tính chất f(-x)=f(x)
Ảnh đẹp thì
Cho hàm số yf(x) liên tục trên K có đạo hàm f(x) Đồ thị của hàm số f(x) như hình vẽ bên. Tìm số điểm cực trị của đồ thị hàm số f(x)? A. 3 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y=f(x) liên tục trên K có đạo hàm f'(x) Đồ thị của hàm số f'(x) như hình vẽ bên.
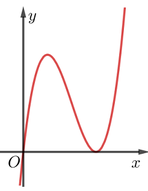
Tìm số điểm cực trị của đồ thị hàm số f(x)?
A. 3
B. 1
C. 0
D. 2
Đáp án B
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
(
x
+
1
)
2
,
x
1
x
2
+
3
,...
Đọc tiếp
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1
- TXĐ: D = R.
+ Với x = 1 ta có f ( 1 ) = k 2
+ Với x ≠ 1 ta có:
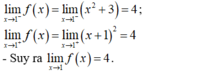
- Vậy để hàm số gián đoạn tại x = 1 khi và chỉ khi:
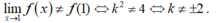
Chọn A
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
(
x
+
1
)
2
,
x
1
x...
Đọc tiếp
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 x = 1 . Tìm k để f(x) gián đoạn tại x= 1.
A. K ≢ ± 2
B. K ≢ 2
C. K ≢ - 2
D. K ≢ ± 1
