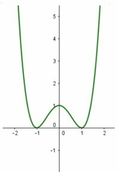
Cho hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. a > 0, b < 0, c > 0
B. a < 0, b > 0, c < 0
C. a < 0, b < 0, c < 0
D. a > 0, b < 0, c < 0
PB
Những câu hỏi liên quan
Cho hàm số y f(x), biết tại các điểm A, B, C đồ thị của hàm số y f(x) có tiếp tuyến được thể hiện như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A
.
f
(
x
C
)
f
(
x
A
)
f
(
x
B
)
....
Đọc tiếp
Cho hàm số y = f(x), biết tại các điểm A, B, C đồ thị của hàm số y = f(x) có tiếp tuyến được thể hiện như hình vẽ bên. Mệnh đề nào dưới đây đúng?
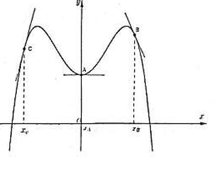
A . f ' ( x C ) < f ' ( x A ) < f ' ( x B ) .
B . f ' ( x A ) < f ' ( x B ) < f ' ( x C ) .
C . f ' ( x A ) < f ' ( x C ) < f ' ( x B ) .
D . f ' ( x B ) < f ' ( x A ) < f ' ( x C ) .
Cho hàm số y f(x) có đạo hàm trên
ℝ
và có đồ thị hàm số y f (x) như hình vẽ bên. Xét hàm số
g
x
f
x
3
-
2
Mệnh đề nào sau đây là sai? A. Hàm số g(x) nghịch biến trên khoảng (-1;0) B. Hàm số g(x) nghịch biến trên khoảng
-
∞
;
-...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên ℝ và có đồ thị hàm số y = f '(x) như hình vẽ bên. Xét hàm số g x = f x 3 - 2 Mệnh đề nào sau đây là sai?
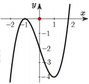
A. Hàm số g(x) nghịch biến trên khoảng (-1;0)
B. Hàm số g(x) nghịch biến trên khoảng - ∞ ; - 2
C. Hàm số g(x) nghịch biến trên khoảng (0;2)
D. Hàm số g(x) đồng biến trên khoảng 2 ; + ∞
Đáp án A.
Ta có g ' x = x 2 - 2 ' f ' x 2 - 2 = 2 x . f ' x 2 - 2 ; ∀ x ∈ ℝ .
Khi đó g ' x < 0 ⇔ x . f ' x 2 - 2 < 0 ⇔ [ x < 0 f ' x 2 - 2 > 0 x > 0 f ' x 2 - 2 < 0 ⇔ [ x < 0 x 2 - 2 > 2 x > 0 x 2 - 2 < 2 ⇔ [ 0 < x < 2 x < - 2 .
Vậy hàm số nghịch biến trên khoảng - ∞ ; - 2 và (0;2) khẳng định A là sai.
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng về hàm số đó?
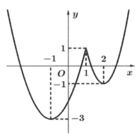
A. Nghịch biến trên khoảng (-1;0)
B. Đồng biến trên khoảng (-3;1)
C. Đồng biến trên khoảng (0;1)
D. Nghịch biến trên khoảng (0;2)
Chọn C
Hàm số đã cho đồng biến trên (0;1)
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đồ thị như hình vẽ bên.Mệnh đề nào sau đây đúng về hàm số đó? A. Nghịch biến trên khoảng (-3;0) B. Đồng biến trên khoảng (0;2) C. Đồng biến trên khoảng (-1;0) D. Nghịch biến trên khoảng (0;3)
Đọc tiếp
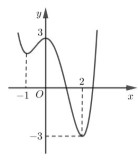
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
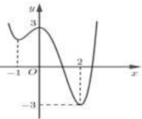
Mệnh đề nào sau đây đúng về hàm số đó?
A. Nghịch biến trên khoảng (-3;0)
B. Đồng biến trên khoảng (0;2)
C. Đồng biến trên khoảng (-1;0)
D. Nghịch biến trên khoảng (0;3)
Cho hàm số yf(x) có đồ thị như hình vẽ bên.Mệnh đề nào sau đây đúng về hàm số đó A. Nghịch biến trên khoảng (-3;0) B. Đồng biến trên khoảng(0;2) C. Nghịch biến trên khoảng (0;3) D. Đồng biến trên khoảng(-1;0)
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây đúng về hàm số đó
A. Nghịch biến trên khoảng (-3;0)
B. Đồng biến trên khoảng(0;2)
C. Nghịch biến trên khoảng (0;3)
D. Đồng biến trên khoảng(-1;0)
Cho hàm số y f(x) có đạo hàm liên tục trên R và hàm số y f’(x) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng? A. Hàm số y f( x) đạt cực đại tại điểm x -1 B. Hàm số y f( x) đạt cực tiểu tại điểm x 1 C. Hàm số y f(x) đạt cực tiểu tại điểm x -2 D. Hàm số y f(x) đạt cực đại tại điểm x -2.
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R và hàm số y= f’(x) có đồ thị như hình vẽ bên.
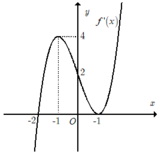
Mệnh đề nào sau đây đúng?
A. Hàm số y= f( x) đạt cực đại tại điểm x= -1
B. Hàm số y= f( x) đạt cực tiểu tại điểm x= 1
C. Hàm số y= f(x) đạt cực tiểu tại điểm x= -2
D. Hàm số y= f(x) đạt cực đại tại điểm x= -2.
Chọn C
+ ta có: f’( x) = 0 khi x= -1 hoặc x= -2.
+ Giá trị của hàm số y= f’(x) không đổi dấu khi đi qua x= - 1 nên x= -1 không là điểm cực trị của hàm số.
+ Giá trị của hàm số y= f’(x) đổi dấu từ âm sang dương khi qua x= -2
=> Hàm số y= f(x) đạt cực tiểu tại điểm x= -2.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng? A. Phương trình f(x)m luôn có nghiệm B. Phương trình f(x)m có hai nghiệm phân biệt nếu m1 C. Phương trình f(x)m có ít nhất hai nghiệm D. Phương trình f(x)0 có hai nghiệm phân biệt
Đọc tiếp
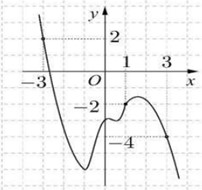
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
A. Phương trình f(x)=m luôn có nghiệm
B. Phương trình f(x)=m có hai nghiệm phân biệt nếu m=1
C. Phương trình f(x)=m có ít nhất hai nghiệm
D. Phương trình f(x)=0 có hai nghiệm phân biệt
Đáp án D
Phương trình y=f(x) có hai nghiệm phân biệt
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị yf(x) như hình vẽ bên. Đặt
g
(
x
)
f
(
x
)
-
x
2
2
biết rằngđồ thị của hàm g(x) luôn cắt trục hoành tại 4 điểm phân biệt. Mệnh đề nào dưới đây đúng A.
g
(...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có
đồ thị y=f'(x) như hình vẽ bên. Đặt g ( x ) = f ( x ) - x 2 2 biết rằng
đồ thị của hàm g(x) luôn cắt trục hoành tại 4 điểm phân biệt.
Mệnh đề nào dưới đây đúng
A. g ( 0 ) > 0 g ( 1 ) < 0 g ( - 2 ) g ( 1 ) > 0
B. g ( 0 ) > 0 g ( 1 ) > 0 g ( - 2 ) g ( 1 ) < 0
C. g ( 1 ) < 0 g ( 0 ) > 0
D. g ( 0 ) > 0 g ( - 2 ) < 0
Cho hàm số yf(x). Đồ thị hàm số yf(x) như hình vẽ bên. Đặt
g
(
x
)
2
f
(
x
)
+
(
x
+
1
)
2
. Mệnh đề nào dưới đây đúng A. maxg(x) trên [-3; 3] g(-3) B. maxg(x) trên [-3; 3] g(2) C. maxg(x) trên [-3; 3] g(1) D. maxg(x) trên [-3; 3] g(-1)
Đọc tiếp
Cho hàm số y=f(x). Đồ thị hàm số y=f'(x) như hình vẽ bên. Đặt g ( x ) = 2 f ( x ) + ( x + 1 ) 2 . Mệnh đề nào dưới đây đúng
A. maxg(x) trên [-3; 3] =g(-3)
B. maxg(x) trên [-3; 3] =g(2)
C. maxg(x) trên [-3; 3] =g(1)
D. maxg(x) trên [-3; 3] =g(-1)
Cho hàm số yf(x) có đạo hàm trên R. Hàm số yf (x) có đồ thị như hình vẽ bên. Xét hàm số
y
f
(
x
2
)
. Mệnh đề nào dưới đây là sai? A. Hàm số g(x) đồng biến trên khoảng (0;1) B. Đồ thị hàm số yg(x) có 5 điểm cực trị C. Hàm số yg(x) đạt cực đại tại x1 D. Đồ thị hàm số yg(x) có 5 điểm cực tiểu
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R. Hàm số y=f '(x) có đồ thị như hình vẽ bên. Xét hàm số y = f ( x 2 ) . Mệnh đề nào dưới đây là sai?
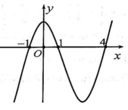
A. Hàm số g(x) đồng biến trên khoảng (0;1)
B. Đồ thị hàm số y=g(x) có 5 điểm cực trị
C. Hàm số y=g(x) đạt cực đại tại x=1
D. Đồ thị hàm số y=g(x) có 5 điểm cực tiểu
