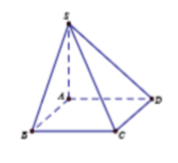
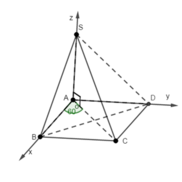
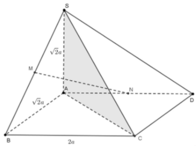
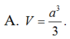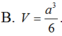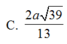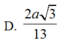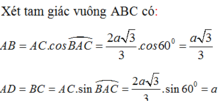Cho hình chóp SABCD có đáy là hình chữ nhật A B = 2 a , A D = 2 a , SA vuông góc với đáy và S A = 2 a Gọi M và N lần lượt là trung điểm của SB và AD( tham khảo hình vẽ). Côsin góc giữa đường thẳng MN và mặt phẳng (SAC) bằng
A. 1 3
B. 3 3
C. 6 3
D. 3 6