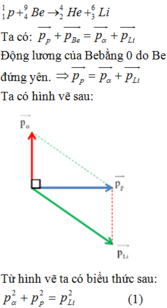
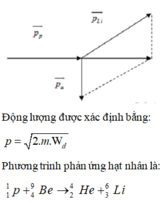
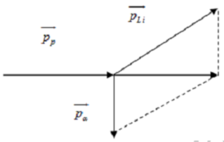
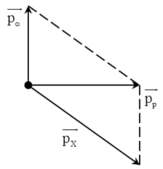
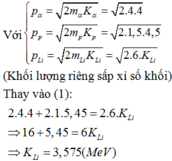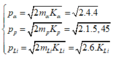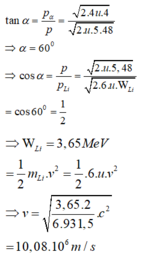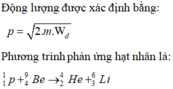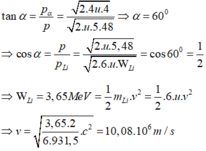Cho hạt prôtôn có động năng K p = 1 , 46 MeV bắn vào hạt nhân Li 3 7 đứng yên. Hai hạt nhân X sinh ra giốn nhau và có cùng động năng. Cho m Li = 7 , 0142 u , m p = 1 , 0073 u m x = 4 , 0015 u góc tạo bởi các vectơ vận tốc của hai hạt X sau phản ứng là
A. 168 0 36 '
B. 48 0 18 '
C. 60 0
D. 70 0