Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = 1 + x + 1 x 2 - 1 - m x + 2 m có hai tiệm cận đứng?
A. 0
B. 2
C. 3
D. 1
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = 1 + x + 1 x 2 - 1 - m x + 2 m có hai tiệm cận đứng?
A. 0
B. 2
C. 3
D. 1
Đáp án C
Yêu cầu bài toán ⇔ x 2 - ( 1 - m ) x + 2 m = 0 có 2 nghiệm phân biệt lớn hơn hoặc bằng -1
Khi và chỉ khi ∆ > 0 x 1 + x 2 + 2 ≥ 0 x 1 + 1 x 2 + 1 ≥ 0 ⇔ 1 - m 2 - 4 . 2 m > 0 1 - m + 2 ≥ 0 2 m + 2 - m + 1 ≥ 0 ⇔ - 2 ≤ m ≤ 5 - 2 6 .
Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 100 ) + m 2 có 5 điểm cực trị?

A. 0.
B. 1.
C. 2.
D. 4.
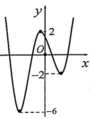
Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f x + 100 + m 2 có 5 điểm cực trị?
A. 0
B. 1
C. 2
D. 4
Chọn đáp án C
Hàm số y=f(x+100) có đồ thị là đồ thị hàm số y=f(x) tịnh tiến sang trái 100 đơn vị
Dựa vào đồ thị ta thấy đồ thị hàm số y=f(x) có 3 điểm cực trị.
Khi tịnh tiến sang trái 100 đơn vị thì số điểm cực trị hàm số y=f(x+100) vẫn là 3 điểm cực trị.

Hình vẽ dưới đây là đồ thị của hàm số y = f x .
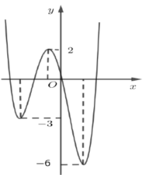
Có bao nhiêu giá trị nguyên dương của tham số để hàm số y = f x + 1 + m có 5 điểm cực trị ?
![]()
![]()
![]()
![]()
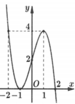
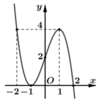
Cho hàm số y = f(x) có đồ thị f’(x) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x = f x 2 + x - 1 + 480 m x 2 + x + 2 nghịch biến trên (0; 1)?
A. 4
B. 6
C. 7
D. 8
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = - x 3 + 3 x 2 + 3 ( m 2 - 1 ) x - 3 m 2 - 1 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
A. 0
B. 1
C. 2
D. 3
+ Đạo hàm y’ = -3x2+ 6x+ 3( m2-1) = -3( x2- 2x-m2+1).
Đặt g( x) = x2- 2x-m2+1 là tam thức bậc hai có ∆ ' = m 2 .
+ Do đó hàm số đã cho có cực đại cực tiểu khi và chỉ khi y’ =0 có hai nghiệm phân biệt hay g(x) =0 có hai nghiệm phân biệt
⇔ ∆ ' > 0 ⇔ m ≠ 0 . (1)
+ Khi đó y’ có các nghiệm là: 1±m .
Tọa độ các điểm cực trị của đồ thị hàm số là A( 1-m ; -2-2m3) và B( 1+m ; -2+ 2m3).
Ta có:
O A → ( 1 - m ; - 2 - 2 m 3 ) ⇒ O A 2 = ( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 . O B → ( 1 + m ; - 2 + 2 m 3 ) ⇒ O B 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 .
Để A và B cách đều gốc tọa độ khi và chỉ khi OA= O B hay OA2= OB2
( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 ⇔ - 4 m + 16 m 3 = 0
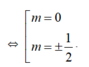
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.
Vậy không có giá trị nguyên nào của m thỏa mãn yêu cầu bài toán.
Chọn A.
Cho hàm số y = f(x) có đồ thị f'(x) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x = f x 2 + x - 1 + 480 m x 2 + x + 2 nghịch biến trên (0;1)?
A. 4
B. 6
C. 7
D. 8
Hàm số g(x) nghịch biến trên khoảng (0;1) khi ![]()
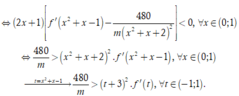
Dựa vào đồ thị, ta có
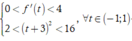
![]()
Theo YCBT 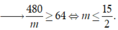
Chọn C.
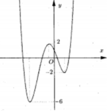
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây: có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 2018 ) + m 2 có 5 điểm cực trị
B. 1
C. 2
D. 3
Có bao nhiêu giá trị nguyên của tham số m sao cho đồ thị của hàm số y = x + 1 m x 2 + 1 có hai tiệm cận ngang.
A. 8
B. 10
C. 12
D. Vô số
Điều kiện: mx2+ 1 > 0.
- Nếu m= 0 thì hàm số trở thành y= x+ 1 không có tiệm cận ngang.
- Nếu m< 0 thì hàm số xác định ⇔ - 1 - m < x < 1 - m
Do đó, lim x → ± ∞ y không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
- Nếu m> 0 thì hàm số xác định với mọi x.
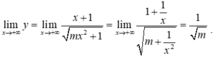
Suy ra đường thẳng y = 1 m là tiệm cận ngang của đồ thị hàm số khi x → + ∞ .

Suy ra đường thẳng y = - 1 m là tiệm cận ngang của đồ thị hàm số khi x → - ∞
Vậy m> 0 thỏa mãn yêu cầu đề bài.
Chọn D.