Biết F(x) là một nguyên hàm của hàm số f ( x ) = 1 2 x - 1 và F ( 2 ) = 3 + 1 2 ln 3 . Tính F(3).
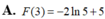
![]()
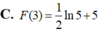
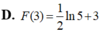
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 2 x - 1 biết F(1)=2. Giá trị của F(2) là
A. F ( 2 ) = 1 2 ln 3 + 2
B. F ( 2 ) = ln 3 + 2
C. F ( 2 ) = 1 2 ln 3 - 2
D. F ( 2 ) = 2 l n 3 - 2
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 2 x - 1 biết F(1)=2. Giá trị của F(2) là:
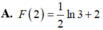
![]()
![]()
![]()
Cho F(x) là một nguyên hàm của hàm số f(x)= 1 2 x - 1 . Biết F(1)=2. Giá trị của F (2) là
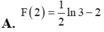
![]()
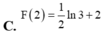
![]()
Biết một nguyên hàm của hàm số f ( x ) = 1 1 - 3 x + 1 là hàm số F ( x ) thỏa mãn F ( - 1 ) = 2 3 . Khi đó F ( x ) là hàm số nào sau đây?
A. F ( x ) = x - 2 3 1 - 3 x + 3
B. F ( x ) = x - 2 3 1 - 3 x - 3
C. F ( x ) = x - 2 3 1 - 3 x + 1
D. F ( x ) = 4 - 2 3 1 - 3 x
Chọn A
F ( x ) = ∫ 1 1 - 3 x + 1 d x = - 1 3 ∫ d ( 1 - 3 x ) 1 - 3 x + x = x - 2 3 1 - 3 x + C
F ( - 1 ) = 2 3 ⇒ C = 3 ⇒ F ( x ) = x - 2 3 1 - 3 x + 3
Biết F(x) là một nguyên hàm của hàm số f(x)= e 2 x và F(0)=3/2. Tính F(1/2)
A. F(1/2)=1/2 e+2
B. F(1/2)=1/2 e+1
C. F(1/2)=1/2 e+1/2
D. F(1/2)=2e+1
Cho F ( x ) là một nguyên hàm của hàm số f ( x ) = 1 2 x - 1 . Biết F 1 = 2 . Giá trị của F (2) là
A. F 2 = 1 2 ln 3 - 2
B. F 2 = ln 3 + 2
C. F 2 = 1 2 ln 3 + 2
D. F 2 = 2 ln 3 - 2
Biết rằng x e x là một nguyên hàm của hàm số f(-x) trên khoảng - ∞ , + ∞ . Gọi F(x) là một nguyên hàm của f ' x e x thỏa mãn F(0) =1, giá trị của F(-1) bằng:
A. 7 2
B. 5 - e 2
C. 7 - e 2
D. 5 2
Đáp án A
Phương pháp:
+) x e x là một nguyên hàm của hàm số nên x e x ' = f ( - x )
+) Từ f ( - x ) ⇒ f ( x )
+) F(x) là một nguyên hàm của f ' x e x ⇒ F ( x ) = ∫ f ' ( x ) e x d x
+) Tính F(x), từ đó tính F(-1)
Cách giải:
Vì x e x là một nguyên hàm của hàm số f ( - x ) nên x e x ' = f ( - x )
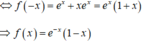
![]()
![]()
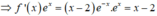
![]()
![]()
![]()
![]()
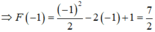
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
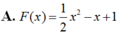
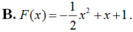
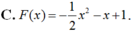
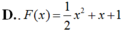
Chọn D.
Ta có
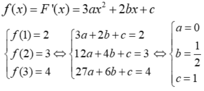
Vậy F(x)= 1 2 x 2 + x + 1
Tìm một nguyên hàm F(x) của hàm số f ( x ) = 1 ( x + 1 ) 2 biết F ( 1 ) = - 1 2
A. 1 - 3 . 1 ( x + 1 ) 2
B. - 1 2 . 1 ( x + 1 ) 2
C. - 3 . 1 ( x + 1 ) 4
D. Cả 3 phương án trên đều sai