Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
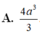
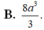
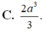
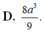
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
A. 4 a 3 3
B. 8 a 3 3
C. 2 a 3 3
D. 8 a 3 9
Đáp án B
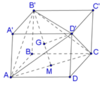
Nhận thấy chóp ACD’B’ có tất cả các cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là trọng tâm của tam giác AB’C’. Chóp ACD’B’ nhận D’G là đường cao.
Xét tam giác AB’C’ có
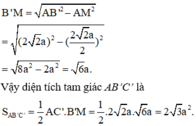
Xét tam giác vuông D’GB’ ta có

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M là trung điểm A’B’, N là trung điểm BC.
Tính thể tích khối tứ diện ADMN
Gọi M’ là hình chiếu của M lên mp(ABCD).

Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng
A. a 3 2 .
B. a 3 3 .
C. a 3 3 2 .
D. a 3 2 3 .
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng:
A . a 3 2
B . a 3 3
C . a 3 3 2
D . a 3 2 3
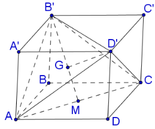
Cho ABCD.A′B′C′D′ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD′B′ là
A. 8 a 3 3
B. 4 a 3 3
C. 2 a 3 3
D. 8 a 3 9
Đáp án C
Nhận thấy chóp ACD′B′ có tất cả các
cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là
trọng tâm của tam giác AB′C′.
Chóp ACD′B′ nhận D′G là đường cao.
Xét tam giác AB′C′ có

Cho khối lập phương ABCD.A’B’C’D’ có cạnh là a. Tính thể tích khối chóp tứ giác D.ABC'D'
A. a 3 3
B. a 3 2 6
C. a 3 2 3
D. a 3 4
Cho hình lập phương ABCD.A’B’C’D’ cạnh 2a, gọi M là trung điểm của BB’ và P thuộc cạnh DD’ sao cho D P = 1 4 D D ' . Mặt phẳng (AMP) cắt CC’ tại N. Thể tích khối đa diện AMNPBCD bằng
A. V = 2 a 3
B. V = 3 a 3
C. V = 9 4 a 3
D. V = 11 3 a 3
Cho hình lập phương ABCD.A’B’C’D; cạnh bằng a. Gọi O là giao điểm của AC và BD. Thể tích của tứ diện OA’BC bằng
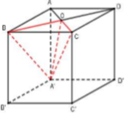
A. a 3 12
B. a 3 24
C. a 3 6
D. a 3 4
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 2a. Một hình trụ có hai đáy là hai hình tròn nội tiếp trong hai hình vuông ABCD và A’B’C’D’. Tính thể tích của khối lăng trụ tạo nên từ hình trụ trên.
A. 2 π a 3 .
B. π a 3 .
C. 2 2 π a 3 .
D. 4 π a 3 .