Gọi I là tâm mặt cầu đi qua 4 điểm M(1; 0; 0), N(0; 1; 0), P(0; 0; 1), Q(1; 1; 1). Tìm tọa độ tâm I.
A. 1 2 ; - 1 2 ; 1 2
B. 2 3 ; 2 3 ; 2 3
C. 1 2 ; 1 2 ; 1 2
D. - 1 2 ; - 1 2 ; - 1 2
PB
Những câu hỏi liên quan
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
Đọc tiếp
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là: A.
(
x
-
1
)
2
+
(
y
+
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là:
A. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 3
B. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9
C. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 3
D. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 9
Trong không gian Oxyz, cho 2 điểm I(1;-2;3), M(0;1;5). Phương trình mặt cầu tâm I và đi qua M là A.
(
x
+
1
)
2
+
(
y
-
2
)
2
+
(
z
+
3
)...
Đọc tiếp
Trong không gian Oxyz, cho 2 điểm I(1;-2;3), M(0;1;5). Phương trình mặt cầu tâm I và đi qua M là
A. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z + 3 ) 2 = 14
B. ( x - 1 ) 2 + y + 2 ) 2 + ( z - 3 ) 2 = 14
C. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 14
D. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 14
Trong không gian Oxyz, cho 2 điểm I(1;-2;3) và M(0;1;5). Phương trình mặt cầu tâm I đi qua M là A.
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
3
)...
Đọc tiếp
Trong không gian Oxyz, cho 2 điểm I(1;-2;3) và M(0;1;5). Phương trình mặt cầu tâm I đi qua M là
A. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 14
B. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z + 3 ) 2 = 14
C. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z + 3 ) 2 = 14
D. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 14
Trong không gian Oxyz cho điểm A(1;0;-1). Gọi (S) là mặt cầu tâm I, đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng
17
2
. Tính bán kính R của mặt cầu (S) A. R3 B. R9 C. R5 D. R1
Đọc tiếp
Trong không gian Oxyz cho điểm A(1;0;-1). Gọi (S) là mặt cầu tâm I, đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S)
A. R=3
B. R=9
C. R=5
D. R=1
Trong không gian Oxyz cho các điểm M(2,1,4); N(5,0,0);
P
1
,
-
3
,
1
. Gọi I(a,b,c) là tâm của mặt cầu tiếp xúc với mặt phẳng (Oyz) đồng thời đi qua các điểm M ,N , P. Tìm c biết rằng
a
+
b
+
c
5
A. 3 B. 2 C. 4 D. 1
Đọc tiếp
Trong không gian Oxyz cho các điểm M(2,1,4); N(5,0,0); P 1 , - 3 , 1 . Gọi I(a,b,c) là tâm của mặt cầu tiếp xúc với mặt phẳng (Oyz) đồng thời đi qua các điểm M ,N , P. Tìm c biết rằng a + b + c < 5
A. 3
B. 2
C. 4
D. 1
Gọi I(a,b,c) là tâm mặt cầu tiếp xúc với (Oyz) đồng thời đi qua M, N, P.
Ta có:
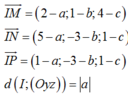
Ta có:
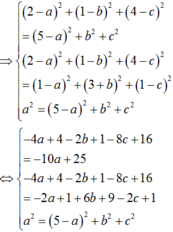
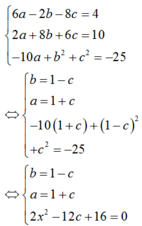
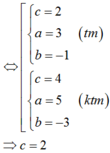
Chọn B.
Đúng 0
Bình luận (0)
Cho mặt cầu (O; R) tiếp xúc với mặt phẳng (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M ta kẻ hai tiếp tuyến của mặt cầu cắt (P) tại A và B. Chứng minh rằng góc (AMB)= góc (AIB)
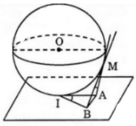
* Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA
Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.
Ta có AM và AI là hai tiếp tuyến cắt nhau tại A của mặt cầu nên:
AM = AI ( tính chất hai tiếp tuyến cắt nhau)
* Tương tự có BM = BI.
* Xét hai tam giác AMB và tam giác AIB có:
AM = AI
BM = BI
AB chung
Suy ra: ∆ AMB = ∆ AIB ( c.c.c)
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, gọi I là tâm mặt cầu đi qua bốn điểm A(2;3;-1), B(-1;2;1), C(2;5;1), D(3,4,5). Tính độ dài đoạn thẳng OI.
Đọc tiếp
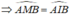
Trong không gian với hệ trục tọa độ Oxyz, gọi I là tâm mặt cầu đi qua bốn điểm A(2;3;-1), B(-1;2;1), C(2;5;1), D(3,4,5). Tính độ dài đoạn thẳng OI.
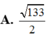
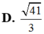
Đáp án C.
Gọi I(a,b,c) là tâm mặt cầu đi qua 4 điểm A(2;3;-1), B(-1;2;1), C(2;5;1), D(3,4,5)
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, gọi I là tâm mặt cầu đi qua bốn điểm A(2; 3;-1), B(-1;2;1), C(2;5;l), D(3;4;5). Tính độ dài đoạn thẳng OI A.
133
2
B.
6
C.
123
3
D.
41
3
Đọc tiếp
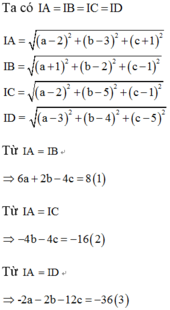
Trong không gian với hệ trục tọa độ Oxyz, gọi I là tâm mặt cầu đi qua bốn điểm A(2; 3;-1), B(-1;2;1), C(2;5;l), D(3;4;5). Tính độ dài đoạn thẳng OI
A. 133 2
B. 6
C. 123 3
D. 41 3
