Cho hai số phức z 1 , z 2 thỏa mãn z 1 + z 2 = 3 5 + 4 5 i , | z 1 - z 2 | = 3 và biểu thức P = 4 | z 1 | 3 + 4 | z 2 | 3 - 3 | z 1 | - 3 | z 2 | + 5 đạt giá trị nhỏ nhất. Tính | z 1 | + | z 2 | .
A. 3
B. 3 4
C. 2
D. 1
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tìm giá trị nhỏ nhất của z - w .
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z − 1 − i = 1 , số phức w thỏa mãn w ¯ − 2 − 3 i = 2 . Tìm giá trị nhỏ nhất của z − w .
A. 17 + 3
B. 13 + 3
C. 13 - 3
D. 17 - 3
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tính giá trị nhỏ nhất của z - w .
A. 13 - 3
B. 17 - 3
C. 17 + 3
D. 13 + 3
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z thỏa mãn z + ( 1 - 2 i ) z = 2 - 4 i . Môđun số phức z bằng bao nhiêu?
A. |z|=3
B. | z | = 5
C. | z | = 5
D. | z | = 4
Cho số phức z thỏa mãn z ( 2 - i ) + 13 i = 1 Tính môđun của số phức z
![]()
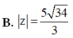
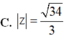
![]()
Cho số phức z thỏa mãn z ( 2 - i ) + 13 i = 1 .Tính môđun của số phức z
A. z = 34
B. z = 5 34 3
C. z = 34 3
D. z = 34
Đáp án D
Phương pháp giải:
Tìm số phức z bằng phép chia số phức, sau đó tính môđun hoặc bấm máy tính
Lời giải: Ta có
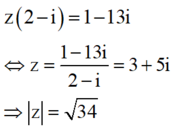
Cho số phức z thỏa mãn z − 1 = z − 2 + 3 i . Tập hợp các điểm biểu diện số phức z là
A. Đường tròn tâm I(1;2), bán kính R = 1
B. Đường thẳng có phương trình 2 x − 6 y + 12 = 0
C. Đường thẳng có phương trình x − 3 y − 6 = 0
D. Đường thẳng có phương trình x − 5 y − 6 = 0
Cho số phức z thỏa mãn z - 1 = z - 2 + 3 i Tập hợp các điểm biểu diễn số phức z là
A. Đường tròn tâm I(1;2), bán kính R = 1.
B. Đường thẳng có phương trình 2x-6y+12=0
C. Đường thẳng có phương trình x-3y-6=0
D. Đường thẳng có phương trình x-5y-6=0
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z
A. | z | = 34
B. | z | = 34
C. | z | = 34 3
D. | z | = 5 34 3