Tính thể tích của khối tứ diện đều có tất cả các cạnh bằng a.
A. 2 12 a 3
B. a 3
C. 6 a 3
D. 1 12 a 3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tính thể tích của khối tứ diện đều có tất cả các cạnh bằng a.
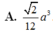
![]()
![]()
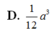
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
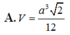
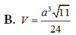
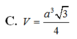
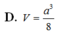
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
A. V = a 3 2 12
B. V = a 3 11 24
C. V = a 3 3 4
D. V = a 3 8
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
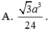
![]()
![]()
![]()
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
A. 3 a 3 24 .
B. 2 π a 3 24 .
C. 2 2 a 3 9 .
D. 3 π a 3 8 .
Đáp án B
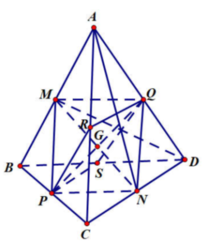
Gọi G là trọng tâm tứ diện ABCD. Ta chứng minh G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện.
Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, BC, AD, AC, BD.
Ta có G là trung điểm của các đoạn MN, PQ, RS.
Δ A C D = Δ B C D ⇒ A N = B N ⇒ Δ N A B cân tại N ⇒ M N ⊥ A B
Tương tụ ta có M N ⊥ C D .
Ta có: P Q = R S = M N = A N 2 − A M 2 = a 3 2 2 − a 2 4 = a 2 2 .
Suy ra d G , A B = d G , C D = 1 2 M N = a 2 4 .
Chứng minh tương tự ta có d G , A C = d G , A D = d G , B D = d G , B C = a 2 4
Vậy G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD.
Bán kính mặt cầu R = a 2 4 . Suy ra thể tích khối cầu là V = 4 3 π R 3 = 4 3 π a 2 4 3 = 2 π a 3 24 .
Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính thể tích khối tứ diện A’BB’C’.
Ta chia khối lẳng trụ đã cho thành hình chóp A’.ABC, C.A’B’C’ và C.A’BB’
Ta có: VA’.ABC = VA’B’C’ = 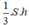 trong đó S là diện tích đáy S = SABC = SA’B’C’ và h là chiều cao của hình lăng trụ
trong đó S là diện tích đáy S = SABC = SA’B’C’ và h là chiều cao của hình lăng trụ
Lại có: VABC.A’B’C’ = S.h
Do đó,
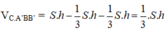
Trong đó, tam giác ABC là tam giác đều có độ dài cạnh bằng a nên 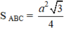
Vì đây là hình lăng trụ đứng nên h = AA’ = BB’= CC’ = a.
Vậy thể tích hình chóp C.A’BB’ là:
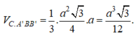
Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Tính thể tích của (H).
A. a 3 3 2
B. a 3 3 4
C. a 3 3
D. a 3 2 6
Đáp án D
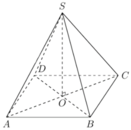
Gọi khối chóp tứ giác đều đó là S. ABCD.
Gọi O là giao điểm hai đường chéo hình vuông ABCD, ta có SO là đường cao hình chóp.
S O = S A 2 - A O 2 = a 2 - a 2 2 2 = a 2 2
S A B C D = a 2
Vậy thể tích cần tìm là:
V = 1 3 . S A B C D . S O = 1 3 a 2 . a 2 2 = a 3 2 6
Thể tích của khối tứ diện đều có tất cả các cạnh bằng 3 là:
A. 6 4
B. 3 6 4
C. 3 3
D. 3 2
Thể tích của khối tứ diện đều có tất cả các cạnh bằng 3 là:
A . 6 4
B . 3 6 4
C . 3 3
D . 3 2