Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy A B = a , A D = a 2 , S A = a 3 . Số đo của góc giữa SC và mặt phẳng (ABCD) bằng
A. 60 0
B. 45 0
C. 30 0
D. 75 0
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. AB=a, BC=2a cạnh bên SA vuông góc với đáy và SA=a 2 Tính thể tích khối chóp S.ABCD
A. 2 3 a 3 3
B. 2 2 a 3 3
C. 2 2 a 3
D. 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy (ABCD). Biết AB=a, BC=3a, SA=2a.Tính thể tích V của khối chóp S.ABCD.
A. V = 3 a 3
B. V = 2 a 3
C. V = a 3
D. V = 6 a 3
Đáp án B
Thể tích khối chóp S.ABCD là:
V A B C D = 1 3 S A . S A B C D = 1 3 2 a .3 a 2 = 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a; AD = 3a. Cạnh bên SA vuông góc với đáy ABCD và SA = a. Tính thể tích V của khối chóp S.ABCD.
A. V=6a3
B. V=a3
C. V=3a3
D. V=2a3.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=2a, BC=a , SA vuông góc với mặt đáy, cạnh SC hợp đáy một góc 30 0 . Thể tích khối chóp S.ABCD tính theo a là:
A. 2 15 a 3 3 .
B. 15 a 3 3 .
C. 2 15 a 3 9 .
Đáp án C
Ta có A C = 2 a 2 + a 2 = a 5 ; S A = A C tan 30 °
= a 5 . 1 3 = a 5 3
Thể tích khối chóp là:
V = 1 3 S A . S A B C D = 1 3 a 5 3 .2 a . a = 2 15 a 3 9
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. A B = a , B C = 2 a cạnh bên SA vuông góc với đáy và S A = a 2 Tính thể tích khối chóp S.ABCD
A. 2 a 3 3 3
B. 2 a 3 2 3
C. 2 a 3 2
D. a 3 2
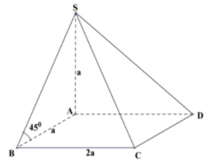
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng
A. 6 a 3 18
B. 2 2 a 3 3
C. a 3 3
D. 2 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy AB=a, AD=a 2 , SA=a 3 . Số đo của góc giữa SC và mặt phẳng (ABCD) bằng
A. 300
B. 450
C. 600
D. 750
Đáp án là B
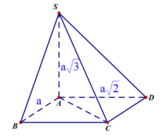
Vì SA vuông góc với đáy nên góc φ giữa SC và mặt phẳng (ABCD) bằng góc giữa SC và hình chiếu AC của nó lên đáy. Suy ra φ = S C A ^ (vì S C A ^ là góc nhọn trong tam giác vuông SAC)
Trong hình chữ nhật ABCD, ta có AC=a 3 . Suy ra tam giác SAC vuông cân ở A.
![]()
Vậy, số đo của góc giữa SC và mặt phẳng (ABCD) bằng 450
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB=2a, AD=3a. Cạnh bên SA vuông góc với đáy (ABCD), SA=a. Tính thể tích V của khối chóp S.ABCD.
![]()
![]()
![]()
![]()
câu 2 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a AD = 2a cạnh SA vuông góc với đáy cạnh SB t
Mặt phẳng (BCM) // AD nên nó cắt mặt phẳng (SAD) theo giao tuyến MN//AD
Ta có: BC ⊥ AB và BC ⊥ SA => BC ⊥ BM
Tứ giác BCNM là hình thang vuông BM là đường cao.
có : BC \(\perp\) AB và BC \(\perp\) SA \(\Rightarrow\) BC \(\perp\) BM
Tứ giác BCNM là hình thang vuông BM là đường cao
ta có : SA = AB . tan 60 = \(a\sqrt{3}\)
\(\dfrac{MN}{AD}=\dfrac{SM}{SA}\)
\(\dfrac{MN}{2a}=\dfrac{a\sqrt{3}-\dfrac{a\sqrt{3}}{3}}{a\sqrt{3}}=\dfrac{2}{3}\)
\(\Rightarrow MN=\dfrac{4a}{3}\)
\(BM=\sqrt{a^2+\dfrac{a^2}{3}}\) \(=\dfrac{2a}{\sqrt{3}}\)
diện tích hình thang BCNM là : \(S=\dfrac{2a+\dfrac{4a}{3}}{2}.\dfrac{2a}{\sqrt{3}}=\dfrac{10a^2}{3\sqrt{3}}\)
\(V_{SBCNM}=\dfrac{1}{3}.SH.S_{BCNM}\)
Hạ SH ⊥ BM
ta có : SH \(\perp\) BM
và BC \(\perp\) (SAB) \(\equiv\) (SBM) \(\Rightarrow\) BC \(\perp\) SH . vậy SH \(\perp\) (BMNC)
\(\Rightarrow\) SH là đường cao của khối chóp S.BCNM
trong \(\Delta SBA\) có \(SB=\dfrac{AB}{cos60}=2a\)
\(\Rightarrow\) \(\dfrac{AB}{SB}=\dfrac{AM}{MS}=\dfrac{1}{2}\)
BM là phân giác của góc : \(\left\{{}\begin{matrix}SBH=gt\\SBH=30^o=gt\\SH=SB.sin30^o=2a.\dfrac{1}{2}=a\end{matrix}\right.\)
\(\Leftrightarrow\) thể tích khói chóp S.BCNM là :
\(V=\dfrac{1}{3}.a.\dfrac{10a^2}{3\sqrt{3}}=\dfrac{10\sqrt{3a^2}}{27}\)
Cho hình chóp S.ABCD có đáy là hình chữ nhật với A B = 2 a , A D = 3 a . Cạnh bên SA vuông góc với đáy ( A B C D ) v à S A = a . Tính thể tích V của khối chóp S.ABCD.
A. V = 6 a 3
B. V = a 3
C. V = 3 a 3
D. V = 2 a 3
: Đáp án D
Thể tích khối chóp là: V = 1 3 S A . S A B C D = 1 3 a .2 a .3 a = 2 a 3 .