Cho hàm số y = f x có đồ thị y = f ' x như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
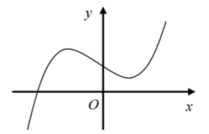
A. 1
B. 2
C. 0
D. 3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hàm số y = f(x) có đạo hàm f'(x) trên khoảng
(
-
∞
;
+
∞
)
. Đồ thị hàm số y = f(x) như hình vẽ 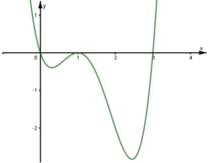
Đồ thị của hàm số y = ( f ( x ) ) 2 có bao nhiêu điểm cực đại, cực tiểu?
A. 2 điểm cực đại, 3 điểm cực tiểu.
B. 1 điểm cực đại, 3 điểm cực tiểu.
C. 2 điểm cực đại, 2 điểm cực tiểu.
A. 3 điểm cực đại, 2 điểm cực tiểu.
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x)=f(x)-x có bao nhiêu điểm cực trị?
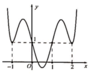
A. 1
B. 2
C. 3
D. 4
Cho hàm số y =f(x) có đạo hàm f’(x) trên khoảng (-∞;+∞). Đồ thị của hàm số y =f(x) như hình vẽ. Đồ thị của hàm số y = f x 2 có bao nhiêu điểm cực đại, điểm cực tiểu?
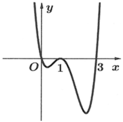
A. 1 điểm cực đại, 3 điểm cực tiểu.
B. 2 điểm cực đại, 3 điểm cực tiểu.
C. 2 điểm cực đại, 2 điểm cực tiểu.
D. 2 điểm cực tiểu, 3 điểm cực đại.
Cho hàm số y = f ( x ) . Hàm số y = f ’ ( x ) có đồ thị như hình vẽ. Hàm số y = f ( x 2 ) có bao nhiêu khoảng nghịch biến.
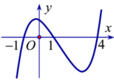
A. 5
B. 3
C. 4
D. 2
Cho hàm số y= f( x) . Hàm số y= f’(x) có đồ thị như hình vẽ
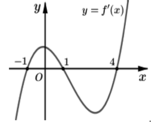
Hàm số y= f( x2) có bao nhiêu khoảng nghịch biến.
A. 5
B. 3
C. 4
D.1
Cho hàm số y= f( x) . Hàm số y= f’ (x) có đồ thị như hình vẽ.
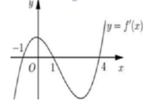
Hàm số y= f( x2) có bao nhiêu khoảng nghịch biến.
A. 5
B . 3
C. 2
D. 4
Ta có g( x) = f( x2) nên g’ (x) = 2x. f’( x2)
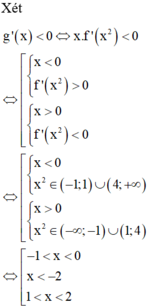
Vậy hàm số đã cho có 3 khoảng nghịch biến.
Chọn B.
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình vẽ bên.
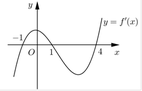
Hàm số y=f( x 2 ) có bao nhiêu điểm cực đại ?
A. 3.
B. 5.
C. 2.
D. 1.
Cho hàm số y=f(x). Hàm số y=f’(x) có đồ thị như hình vẽ bên. Hàm số y = f x 2 có bao nhiêu khoảng nghịch biến?
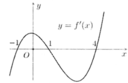
A. 5
B. 3
C. 4
D. 2
Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y = f'(x) như hình vẽ. Hàm số y = f ( 2 x 2 + x ) có bao nhiêu cực trị?
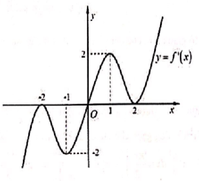
A. 4.
B. 5.
C. 3.
D. 1.
Cho hàm số y = a x 3 + b x 2 + c x + d có đạo hàm là hàm số y=f'(x) có đồ thị như hình vẽ bên.
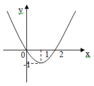
Biết rằng đồ thị hàm số y=f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng bao nhiêu?
A. 2 3
B. 1
C. 3 2
D. 4 3
Đáp án D
Ta có: y ' = 3 a x 2 + 2 b x + c
+) Đồ thị hàm số f'(x) đi qua gốc tọa độ => c=0
+) Đồ thị hàm số f'(x) có điểm cực trị:
1 ; − 1 ⇒ 6 a + 2 b = 0 3 a + 2 b = − 1 ⇔ a = 1 3 b = − 1
Vậy hàm số f ' x = x 2 − 2 x . Đồ thị hàm số f(x) tiếp xúc với trục hoành nên có cực trị nằm trên trục hoành. Các giá trị cực trị của hàm số f(x) là:
f 0 = d f 2 = 8 3 − 4 + d = − 4 3 + d
do điểm tiếp xúc có hoành độ dương
=> d = 4 3 => f(x) cắt trục tung tại điểm có tung độ 4 3