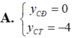
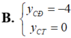
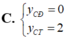
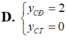
Tìm tung độ các điểm cực đại ( y C D ) và điểm cực tiểu y C T của đồ thị hàm số y = x 2 x - 1
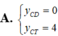
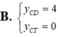
Tìm y C D (tung độ điểm cực đại) và y C T (tung độ điểm cực tiểu) của đồ thị hàm số y = x 2 - 3 x + 3 x - 1
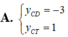
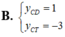
Tìm tung độ điểm cực đại y C N hoặc tung độ điểm cực tiểu Y C T nếu có của hàm số y = x 2 + 1 x + 2
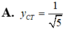
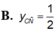
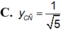
Tìm tung độ điểm cực tiểu của (C): y = 3 x 2 3 - 2 x
Tìm hoành độ các điểm cực đại x C Đ và hoành độ các điểm cực tiểu x C T nếu có của đồ thị y=cos2x.
Tìm tất cả các giá trị của tham số a để hàm số y = x 3 + 3 3 ax có cực đại, cực tiểu và đường thẳng đi qua các điểm cực đại, cực tiểu của đồ thị hàm số đi qua gốc tọa độ
A. a < 0
B. a < -1
C. -1 < a < 0
D. a > 0
Tìm tất cả các giá trị của tham số a để hàm số y = x 3 + 3 3 a x có cực đại, cực tiểu và đường thẳng đi qua các điểm cực đại, cực tiểu của đồ thị hàm số đi qua gốc tọa độ
A. a < -1
B. a < 0
C. -1 < a < 0
D. a > 0
Đáp án B
Ta có y ' = 3 x 2 + 3 3 a
Hàm sổ có cực trị ⇔ y ' = 0 có 2 nghiệm phân biệt ⇔ a < 0 .
Hàm số là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc tọa độ, do đó đường thẳng nối cực đại và cực tiểu của đồ thị hàm số luôn đi qua gốc tọa độ.
Cho hàm số y = 2 3 x 3 + m + 1 x 2 + m 2 + 4 m + 3 x - 3 (m là tham số thực). Tìm điều kiện của m để hàm số có cực đại và cực tiểu và các điểm cực trị của hàm số nằm bên phải của trục tung
A. - 5 < m < - 1
B. - 5 < m < - 3
C. - 3 < m < - 1
D. [ m > - 1 m < - 5
Đáp án B.
Ta có y ' = 2 x 2 + 2 m + 1 x + m 2 + 4 m + 3 ; ∀ x ∈ ℝ .
Phương trình y ' = 0 ⇔ 2 x 2 + 2 m + 1 x + m 2 + 4 m + 3 = 0 (*).
Để hàm số đã cho có 2 điểm cực trị ⇔ (*) có 2 nghiệm phân biệt ⇔ ∆ ' > 0 ⇔ - 5 < m < - 1 .
Và các điểm cực trị của hàm số nằm bên phải Oy ⇔ m 2 + 4 m + 3 > 0 ⇔ [ m > - 1 m < - 3 .
Vậy - 5 < m < - 3 là giá trị cần tìm.
Cho ( C ) : y = x 2 + 5 x - 1 . Gọi là hoành độ các điểm cực tiểu, cực đại của (C). Khi đó
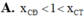
