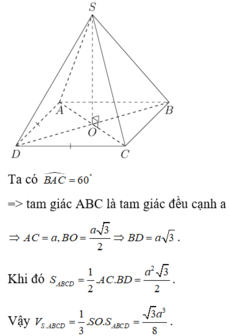
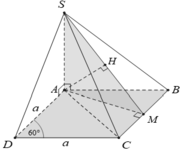
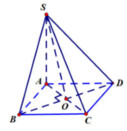
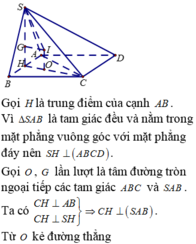
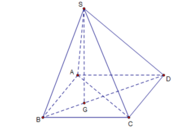
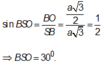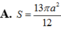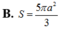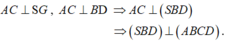Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 0 . Hai mặt bên (SAD) và (SAB) cùng vuông góc với đáy (ABCD) . Cạnh S B = a 2 . Mệnh đề nào dưới đây sai?
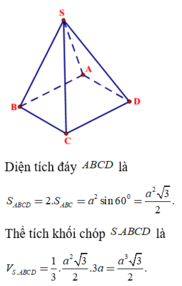
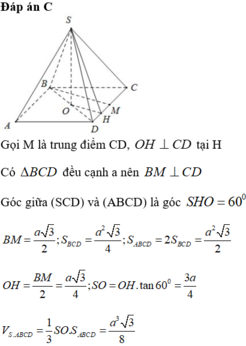
A. S A B C D = a 2 3 2
B. S C = a 2
C. S A C ⊥ S B D
D. V S . A B C D = a 3 3 12