Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 2 x + 1 4 - x 2 là:
A. 2
B. 1
C. 3
D. 4
PB
Những câu hỏi liên quan
Xét các mệnh đề sau(1). Đồ thị hàm số
y
1
2
x
-
3
có hai đường tiệm cận đứng và một đường tiệm cận ngang(2). Đồ thị hàm số
y
x
+
x
2
+
x
+
1...
Đọc tiếp
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Đáp án D
Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
Đồ thị hàm số y = x + x 2 + x + 1 x có 1 tiệm cận đứng là x = 0
Mặt khác lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0 nên đồ thị hàm số có 2 tiệm cận ngang
Xét hàm số y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2 suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng
Đúng 0
Bình luận (0)
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = \(\dfrac{x+\sqrt{x^2+1}}{x+1}\)
Lời giải:
TXĐ: \((-\infty; -1)\cup (-1;+\infty)\)
\(\lim\limits_{x\to +\infty}y=\lim\limits_{x\to +\infty}\frac{1+\sqrt{1+\frac{1}{x}}}{1+\frac{1}{x}}=\frac{1+1}{1}=2\)
\(\lim\limits_{x\to -\infty}y=\lim\limits_{x\to -\infty}\frac{-1+\sqrt{1+\frac{1}{x^2}}}{-1+\frac{1}{-x}}=\frac{-1+1}{-1}=0\)
Do đó ĐTHS có 2 TCN là $y=0$ và $y=2$
\(\lim\limits_{x\to -1-}y=\lim\limits_{x\to -1-}\frac{x+\sqrt{x^2+1}}{x+1}=-\infty\) do \(\lim\limits_{x\to -1-}(x+\sqrt{x^2+1})=\sqrt{2}-1>0\) và \(\lim\limits_{x\to -1-}\frac{1}{x+1}=-\infty\)
Tương tự \(\lim\limits_{x\to -1+}y=+\infty\) nên $x=-1$ là TCĐ của đths
Vậy có tổng 3 TCN và TCĐ
Đúng 1
Bình luận (0)
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
x
+
3
x
-
1
x
2
-
1
là A. 1. B. 2. C. 3 D. 4.
Đọc tiếp
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = x + 3 x - 1 x 2 - 1 là
A. 1.
B. 2.
C. 3
D. 4.
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số
y
2
x
2
-
1
+
1
x
là A. 1. B. 0. C. 2. D. 3.
Đọc tiếp
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số y = 2 x 2 - 1 + 1 x là
A. 1.
B. 0.
C. 2.
D. 3.
ĐKXĐ:
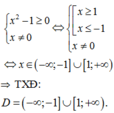
Do đó đồ thị hàm số không có TCĐ.
Ta có:
Vậy đồ thị hàm số có 2 TNN là y = ± 2
Chọn C.
Chú ý: HS có thể sử dụng chức năng CALC trên MTCT để tính giới hạn của hàm số.
Đúng 0
Bình luận (0)
Tổng số các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
x
+
2
16
−
x
4
là A. 3. B. 0. C. 2. D. 1.
Đọc tiếp
Tổng số các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = x + 2 16 − x 4 là
A. 3.
B. 0.
C. 2.
D. 1.
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
2
x
-
1
x
2
-
1
là A. 4. B. 3. C. 1. D. 2.
Đọc tiếp
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = 2 x - 1 x 2 - 1 là
A. 4.
B. 3.
C. 1.
D. 2.
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
x
2
-
1
x
-
1
bằng A. 2. B. 1. C. 4. D. 3.
Đọc tiếp
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x 2 - 1 x - 1 bằng
A. 2.
B. 1.
C. 4.
D. 3.
Chọn đáp án D.
lim x → 1 + y = + ∞ ⇒ x = 1
Đúng 0
Bình luận (0)
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
x
2
-
1
x
-
1
bằng A. 2. B. 1. C. 4. D. 3.
Đọc tiếp
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x 2 - 1 x - 1 bằng
A. 2.
B. 1.
C. 4.
D. 3.
Tìm số phát biểu đúng trong các phát biểu sau:(1) Đồ thị hàm số y
x
α
với
α
0
nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.(2) Đồ thị hàm số y
x
α
với
α
0
không có tiệm cận.(3) Đồ thị hàm số
y
log
a
x
với
1
a...
Đọc tiếp
Tìm số phát biểu đúng trong các phát biểu sau:
(1) Đồ thị hàm số y= x α với α > 0 nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.
(2) Đồ thị hàm số y= x α với α > 0 không có tiệm cận.
(3) Đồ thị hàm số y = log a x với 1 < a ≠ 1 nhận trục Oy làm tiệm cận đứng và không có tiệm cận ngang.
(4) Đồ thị hàm số y=ax với 1 < a ≠ 1 nhận trục Ox làm tiệm cận ngang và không có tiệm cận đứng.
A. 2.
B. 1
C. 4
D. 3.
Phương pháp:
Dựa vào các tính chất của đồ thị hàm số mũ và hàm số logarit.
Cách giải:
Cả 4 phát biểu đều đúng
Chọn C
Đúng 0
Bình luận (0)
Đồ thị của hàm số
y
f
(
x
)
cos
x
+
1
(
x
-
1
)
(
x
-
2
)
có tổng tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? A. 0 B. 3 C. 2 D. 1
Đọc tiếp
Đồ thị của hàm số y = f ( x ) = cos x + 1 ( x - 1 ) ( x - 2 ) có tổng tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. 0
B. 3
C. 2
D. 1
