Gọi S là tập các giá trị của tham số m sao cho phương trình x + 1 3 + 3 - m = 3 3 x + m 3 có đúng hai nghiệm thực. Tính tổng tất cả các phần tử trong tập hợp S
A. 4
B. 2
C. 6
D. 5
Gọi S là tập hợp các giá trị thực của tham số m sao cho phương trình ( x + 1 ) 3 + 3 - m = 3 3 x + m 3 có đúng nghiệm thực. Tích tất cả các phần tử của tập hợp S là
A. -1
B. 1
C. 3
D. 5
Cho phương trình 1 5 x 2 − 4 x + 3 = m 4 − m 2 + 1 . Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình có bốn nghiệm phân biệt. Mệnh đề nào dưới đây đúng?
A. S là một khoảng
B. S là một đoạn
C. S là hợp của hai đoạn rời nhau
D. S là hợp của hai khoảng rời nhau
Cho phương trình 1 5 x 2 − 4 x + 3 = m 4 − m 2 + 1 . Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình có bốn nghiệm phân biệt. Mệnh đề nào dưới đây đúng?
A. S là một khoảng
B. S là một đoạn
C. S là hợp của hai đoạn rời nhau
D. S là hợp của hai khoảng rời nhau
Đáp án D.
ta có m 4 − m 2 + 1 = m 2 − 1 2 2 + 3 4 ≥ 3 4 ∀ m
1 5 x 2 − 4 x + 3 = m 4 − m 2 + 1 ⇔ x 2 − 4 x + 3 = − log 4 m 4 − m 2 + 1
Xét hàm số y = x 2 − 4 x + 3 có bảng biến thiên:
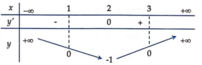
Suy ra bảng biến thiên của hàm số y = x 2 − 4 x + 3 :
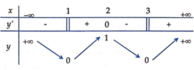
Phương trình x 2 − 4 x + 3 = − log 5 m 4 − m 2 + 1 có 4 nghiệm phân biệt
⇔ 0 < − log 5 m 4 − m 2 + 1 < 1 ⇔ − 1 < log 5 m 4 − m 2 + 1 < 0
⇔ 1 5 < m 4 − m 2 + 1 < 1 ⇔ m 4 − m 2 + 1 < 1
( do m 4 − m 2 + 1 ≥ 3 4 > 1 5 )
⇔ m 4 − m 2 < 0 ⇔ m 2 m 2 − 1 < 0 ⇔ m ≠ 0 m 2 − 1 < 0 ⇔ m ≠ 0 − 1 < m < 1
⇔ m ∈ − 1 ; 0 ∪ 0 ; 1
Vậy S = − 1 ; 0 ∪ 0 ; 1 , tức là S là hợp của hai khoảng với nhau. Vậy D là đáp án đúng.
Gọi S = − ∞ ; a b (với a b là phân số tối giản, a ∈ Z , b ∈ N * ) là tập hợp tất cả các giá trị của tham số m sao cho phương trình 2 x 2 + m x + 1 = x + 3 có hai nghiệm phân biệt. Tính B = a 2 − b 3 .
A. B = 334.
B. B = − 440 .
C. B = 1018.
D. B = 8.
Đáp án A.
Phương trình đã cho tương đương với:
2 x 2 + m x + 1 = x 2 + 6 x + 9 x ≥ − 3 ⇔ x 2 + m − 6 x − 8 = 0 1 x ≥ − 3
Để phương trình có hai nghiệm phân biệt thì (1) phải có 2 nghiệm phân biệt x 2 > x 1 ≥ − 3
⇔ Δ > 0 x 1 + x 2 ≥ − 6 x 1 + 3 x 2 + 3 ≥ 0 ⇔ m − 6 2 + 32 > 0 − m − 6 ≥ − 6 − 8 + 3. − m + 6 + 9 ≥ 0 ⇔ 6 − m ≥ − 6 19 − 3 m ≥ 0 ⇔ m ≤ 12 m ≤ 19 3 ⇔ m ≤ 19 3
Do đó
a b = 19 3 ⇒ a = 19 b = 3 ⇒ B = a 2 − b 3 = 19 2 − 3 3 = 334.
Cho hàm số y = f x có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của tham số m để bất phương trình x m - 2 f sin x + 2 . 2 f sin x + m 2 - 3 . 2 f x - 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Số tập con của tập hợp S là

A. 4
B. 1
C. 2
D. 3
Gọi S là tập hợp giá trị thực của tham số m sao cho phương trình z 2 - m + 4 z + m 2 + 3 = 0 có nghiệm phức z 0 thỏa mãn z 0 = 2 . Số phần tử của tập hợp S là
A. 4
B. 3
C. 2
D. 1
Cho phương trình 4 x − m .2 x + 1 + m + 2 = 0 , m là tham số. Gọi S là tập hợp các giá trị của m sao cho phương trình trên có hai nghiệm dương phân biệt. Biết S là một khoảng có dạng (a;b) tính a-b
A. 1
B. 3
C. 4
D. 2
Đáp án A
Đặt t = 2 x > 0 ⇒ t 2 − 2 m t + m + 2 = 0
ĐK PT có 2 nghiệm phân biệt là: Δ ' = m 2 − m − 2 > 0 S = 2 m > 0 P = m + 2 > 0 ⇔ m > 2
Khi đó: 2 x 1 = t 1 2 x 2 = t 2 ⇒ x 1 = log 2 t 1 ; x 2 = log 2 t 2
Để x 1 ; x 2 > 0 ⇔ t 1 > 1 ; t 2 > 1 ⇔ t 1 + t 2 > 2 t 1 − 1 t 2 − 1 > 0 ⇔ 2 m > 2 m + 2 − 2 m + 1 > 0 ⇔ 1 < m < 3
Vậy m ∈ 2 ; 3
Cho phương trình 4 x - m . 2 x + 1 + m + 2 với m là tham số. Gọi S là tập hợp các giá trị của m sao cho phương trình trên có hai nghiệm dương phân biệt. Biết S là một khoảng có dạng a , b . Tính b - a
A. 1.
B. 3.
C. 4.
D. 2.
Chọn đáp án A
Ta có
![]()
![]()
Đặt t = 2 x > 0 thì phương trình đã cho trở thành t 2 - 2 m . t + m + 2 = 0 *
Để phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi phương trình (*) có hai nghiệm t 1 , t 2 lớn hơn 1.
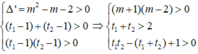
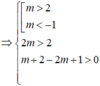
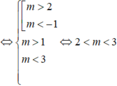
![]()
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x.2x = x(x - m +1) + m(2x - 1) có hai phần tử.Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Đáp án D
Ta có

Giải (1) , đặt f(x) = 2x - x - 1. Xét hàm số f(x) = 2x - x - 1trên R, có f’(x) = 2x.ln2 - 1
Phương trình
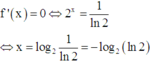
=> f(x) = 0 có nhiều nhất 2 nghiệm mà f(0) = f(1) => f(x) = 0 <=> x = 0 hoặc x = 1
Để phương trình đã cho có hai nghiệm phân biệt <=> (2) có 1 nghiệm hoặc 0
Vậy m = {0 ;1} là hai giá trị cần tìm.