Trong không gian Oxyz, cho 2 véc tơ a → ( 1 ; - 5 ; 2 ) , b → ( 2 ; - 4 ; 0 ) Tính tích vô hướng của 2 véc tơ a → và b → .
A. a → . b → = - 22
B. a → . b → = 22
C. a → . b → = 11
D. a → . b → = - 11
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ ![]() =(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ
=(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ![]() ?
?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho ba véc tơ a → ( 5 ; 7 ; 2 ) , b → ( 3 ; 0 ; 4 ) , c → ( - 6 ; 1 ; - 1 ) . Hãy tìm véc tơ n → = 3 a → - 2 b → + c →
A. (3; 22; -3)
B. (-3; 22; 3)
C. (3; -22; 3)
D. (3; -22; -3)
#2H3Y1-1~Trong không gian Oxyz, cho véc-tơ ![]() sao cho
sao cho ![]() . Tọa độ của véc-tơ
. Tọa độ của véc-tơ ![]() là:
là:
A. (-2;1;2)
B. (1;2;-2)
C. (2;1-2)
D. (2;1;2).
Trong không gian Oxyz, cho hai véc tơ a → = − 4 ; 5 ; − 3 và b → = 2 ; − 2 ; 3 .
.Véc tơ x → = a → + 2 b → có tọa độ là
A. − 2 ; 3 ; 0
B. 0 ; 1 ; − 1
C. 0 ; 1 ; 3
D. − 6 ; 8 ; − 3
C
a → = − 4 ; 5 ; − 3 , b → = 2 ; − 2 ; 3
⇒ 2 b → = 4 ; − 4 ; 6
Có x → = a → + 2 b → suy ra tọa độ của vectơ x → = 0 ; 1 ; 3
Trong không gian Oxyz, cho ba véc tơ a ⇀ ( 5 ; 7 ; 2 ) , b ⇀ ( 3 ; 0 ; 4 ) , c ⇀ ( - 6 ; 1 ; - 1 ) Hãy tìm véc tơ n ⇀ = 3 a ⇀ - 2 b ⇀ + c ⇀ .
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho ba véc tơ a → 5 ; 7 ; 2 , b → 3 ; 0 ; 4 , c → - 6 ; 1 ; - 1 . Hãy tìm véc tơ n → = 3 a → - 2 b → + c → .
A. n → = 3 ; 22 ; - 3
B. n → = - 3 ; 22 ; 3
C. n → = 3 ; - 22 ; 3
D. n → = 3 ; - 22 ; - 3
Trong không gian Oxyz, cho véc tơ a → biểu diễn của các véc tơ đơn vị là a → = 2 i → + k → − 3 j → . Tọa độ của véc tơ a → là:
A. 1 ; 2 ; − 3
B. 2 ; − 3 ; 1
C. 2 ; 1 ; − 3
D. 1 ; − 3 ; 2
Trong không gian Oxyz, cho véc tơ a → biểu diễn của các véc tơ đơn vị là a → = 2 i → + k → - 3 j → . Tọa độ của véc tơ a → là:
A. (1;2;-3)
B. (2;-3;1)
C. (2;1;-3)
D. (1;-3;2)
Trong không gian tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y - 1 - 1 = z - 1 1 Véc tơ nào trong các véc tơ sau đây không là véc tơ chỉ phương của đường thẳng d?
A. u 1 → =(-2;2;-2)
B. u 1 → =(-3;3;-3)
C. u 1 → =(2;-4;4)
D. u 1 → =(1;1;1)
Đáp án D
Phương pháp:
Đường thẳng
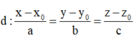
có 1 VTCP là u 1 → =(a;b;c). Mọi vectơ v → =k u → (k ∈ Z)cùng phương với vecto u → đều là VTCP của đường thẳng d.
Cách giải: Đường thẳng d nhận u → =(1;-1;1) là 1 VTCP. Mọi vecto cùng phương với vecto đều là VTCP của đường thẳng d.
Ta thấychỉ có đáp án D, vecto u 1 → =(1;1;1) không cùng phương với u → =(1;-1;1) nên u 1 → =(1;1;1) không là VTCP của đường thẳng d.