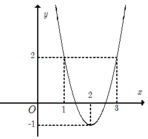
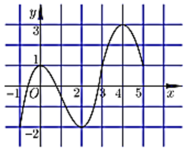
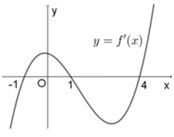
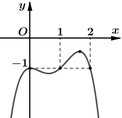
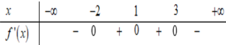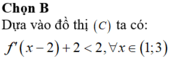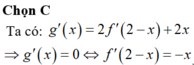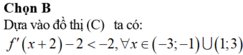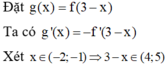Cho hàm số y=f(x) có đạo hàm trên (a;b). Phát biểu nào sau đây là đúng ?
A. Hàm số ![]() không đổi khi và chỉ khi
không đổi khi và chỉ khi ![]() .
.
B. Hàm số ![]() đồng biến khi và chỉ khi
đồng biến khi và chỉ khi ![]() và
và ![]() tại hữu hạn giá trị
tại hữu hạn giá trị ![]()
C. Hàm số ![]() nghịch biến khi và chỉ khi
nghịch biến khi và chỉ khi ![]() .
.
D. Hàm số ![]() đồng biến khi và chỉ khi
đồng biến khi và chỉ khi ![]() .
.