Đường cong trong hình bên là đồ thị của hàm số y = a x + b c x + d với a,b,c,d là các số thực. Mệnh đề nào dưới đây đúng?
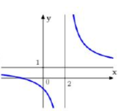
A. y ' < 0 , ∀ x ≠ 1
B. y ' > 0 , ∀ x ≠ 2
C. y ' > 0 , ∀ x ≠ 1
D. y ' < 0 , ∀ x ≠ 2
Cho hàm số f x = x 3 + a x + b và g x = f c x 2 + d x với a , b , c , d ∈ R có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x). Diện tích hình phẳng giới hạn bởi hai đường cong y=f(x) và y=g(x) gần nhất với kết quả nào dưới đây?

A. 7,66
B. 4,24
C. 3,63
D. 5,14
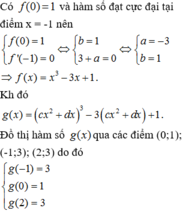

S = ∫ - 1 2 x 2 - x 3 - 3 x 2 - x + 1 - x 3 - 3 x + 1 d x
![]()
Cho hàm số y = f ( x ) = x 3 - 3 x 2 + 2 có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số y = x + 1 ?
A. 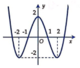
B. 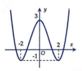
C. 
D. 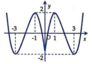
Đáp án C.
Tịnh tiến đồ thị hàm số y = f x sang trái 1 đơn vị.
Giữ nguyên phần đồ thị hàm số nằm bên phải trục tung. Xóa phần đồ thị hàm số nằm bên trái trục tung.
Lấy đối xứng phần đồ thị hàm số nằm bên phải trục tung qua trục tung.
Từ đây ta có đồ thị hàm số y = f x + 1 .
Biết rằng hàm số y = f (x) = a x 4 + b x 2 + c có đồ thị là đường cong trong hình vẽ bên.

Tính giá trị f (a + b + c)
A. f (a + b + c) = -2
B. f (a + b + c) = 2
C. f (a + b + c) = -1
D. f (a + b + c) = 1
Cho f x = x 3 + a x 2 + b x + c và g x = f d x + e với a , b , c , d , e ∈ R có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x). Diện tích hình phẳng giới hạn bởi hai đường cong y=f(x) và y=g(x) gần nhất với kết quả nào dưới đây?
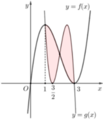
A. 4,5.
B. 4,25.
C. 3,63.
D. 3,67.
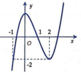
Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số ở phương án A, B, C, D dưới đây?
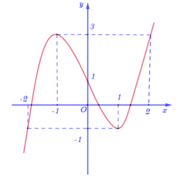
A. y = x 3 - 3 x + 1
B. y = - x 3 - 3 x 2 + 1
C. y = - x 3 - 3 x 2 - 1
D. y = x 3 - 3 x - 1
Chọn A
Từ đồ thị ta thấy hệ số a > 0 do nhánh phải hướng lên trên. Do đó loại B và C.
Mặt khác đồ thị cắt trục tung tại A(0;1). Do đó chọn A.
Đường cong trong hình bên là đồ thị của hàm số y = a x + b c x + d với a , b , c , d là các số thực. Mệnh đề nào dưới đây đúng?
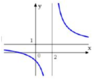
A. y ' < 0 , ∀ x ≠ 1
B. y ' > 0 , ∀ x ≠ 2
C. y ' > 0 , ∀ x ≠ 1
D. y ' < 0 , ∀ x ≠ 2
Chọn D.
Phương pháp
Quan sát và nhận xét dáng đồ thị hàm số, từ đó suy ra tính đồng biến nghịch biến và dấu của y ' .
Cách giải:
Từ đồ thị hàm số ta thấy hàm số nghịch biến trên các khoảng - ∞ ; 2 và 2 ; + ∞ .
Vậy y ' < 0 , ∀ x ≠ 2 .
Cho hàm số y=f(x) xác định và liên tục trên R và có đồ thị là đường cong trong hình vẽ bên.
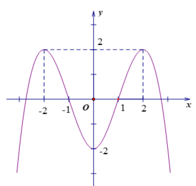
Hỏi điểm cực tiểu của đồ thị hàm số y= f(x) là điểm nào ?
A. x=-2
B. y=-2
C. ![]()
D. ![]()
Chọn C.
Vì đề bài hỏi điểm cực tiểu của đồ thị hàm số, dựa hình vẽ ta thấy điểm ![]() là điểm cực tiểu của đồ thị hàm số.
là điểm cực tiểu của đồ thị hàm số.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các phương án A, B, C, D?
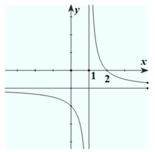
A. y = x + 2 1 - x
B. y = x - 2 1 - x
C. y = x - 1 2 - x
D. y = x + 1 2 - x
Chọn B
Đồ thị hàm số đi qua điểm có tọa độ (2;0) nên ta loại các đáp án A, C, D.
Vậy chọn đáp án B.
Đường cong cong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?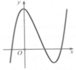
![]()
![]()
![]()
![]()