Cho hình chóp S.ABC có cạnh S A ⊥ A B C , tam giác ABC đều và A B = a ; góc giữa SB và mặt phẳng (ABC) bằng 60 o . Gọi M,N lần lượt là trung điểm của SA,SB. Tính thể tích khối chóp S . M N C :
A. a 3 16
B. a 3 4
C. a 3 3 12
D. a 3 8
PB
Những câu hỏi liên quan
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SAB) vuông góc với mặt phẳng (ABC) và tam giác SAB vuông cân tại S. Tính thể tích khối chóp S.ABC theo a
A
.
a
3
3
12
B
.
a
3
3
24...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SAB) vuông góc với mặt phẳng (ABC) và tam giác SAB vuông cân tại S. Tính thể tích khối chóp S.ABC theo a
A . a 3 3 12
B . a 3 3 24
C . a 3 3 3
D . a 3 3 4
Đáp án B
Vì tam giác SAB cân tại S nên hạ SH ⊥ AB => H là trung điểm của AB.
Vì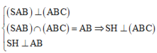 
Tam giác SAB vuông cân tại S nên SA = SB = a 2
Đúng 0
Bình luận (0)
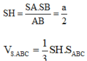
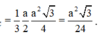
Cho hình chóp tam giác đều S.ABC có AC = SC = 8 cm , SH = 6,93 cm ,S tam giác ABC = 27,72 cm2
a) Cho biết độ dài trung đoạn của hình chóp S.ABC.
b) Tính diện tích xung quanh và diện tích toàn phần của hình chóp S.ABC.
c) Tính thể tích của hình chóp tam giác đều S.ABC biết chiều cao của hình chóp là 7,5 cm
a) Độ dài trung đoạn của hình chóp S.ABC là độ dài đoạn thẳng từ trung điểm của cạnh đáy đến đỉnh của hình chóp. Vì tam giác ABC là tam giác đều, nên ta có thể tính độ dài trung đoạn bằng cách sử dụng công thức Pythagoras: Trung đoạn = căn bậc hai của (AC^2 - (AC/2)^2) = căn bậc hai của (8^2 - (8/2)^2) = căn bậc hai của (64 - 16) = căn bậc hai của 48 = 4 căn 3 cm
b) Diện tích xung quanh của hình chóp S.ABC là tổng diện tích các mặt bên của hình chóp. Vì tam giác ABC là tam giác đều, nên diện tích mặt bên của hình chóp là diện tích tam giác đều. Ta có công thức tính diện tích tam giác đều: Diện tích tam giác đều = (cạnh^2 * căn 3) / 4 = (8^2 * căn 3) / 4 = 16 căn 3 cm^2
Diện tích xung quanh = Diện tích tam giác đều + Diện tích đáy = 16 căn 3 + 27,72 = 16 căn 3 + 27,72 cm^2
Diện tích toàn phần của hình chóp là tổng diện tích xung quanh và diện tích đáy: Diện tích toàn phần = Diện tích xung quanh + Diện tích đáy = 16 căn 3 + 27,72 + 27,72 = 16 căn 3 + 55,44 cm^2
c) Thể tích của hình chóp tam giác đều S.ABC được tính bằng công thức: Thể tích = (Diện tích đáy * Chiều cao) / 3 = (27,72 * 7,5) / 3 = 69,3 cm^3
Đúng 0
Bình luận (1)
cho hình chóp S.ABC có đáy ABC đều cạnh a, tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với (ABC) tính thể tích khối chóp S.ABC.
cho hình chóp S.ABC có đáy ABC đều cạnh a, tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với (ABC) tính thể tích khối chóp S.ABC.
Ai đó giúp mk vứi thay câu hỏi thành tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác vuông tại A,
A
B
C
^
30
0
, SAB là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Thể tích của khối chóp S.ABC là: A.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, A B C ^ = 30 0 , SAB là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Thể tích của khối chóp S.ABC là:
A. a 3 3 9
B. a 3 18
C. a 3 3 3
D. a 3 12
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng (SBC) là
6
4
, từ B đến mặt phẳng (SAC) là
15
10
từ C đến mặt phẳng (SAB) là
30
20
và hình chiếu vuông góc của S xuống đáy nằm trong tam giác ABC. Thể tích khối chóp S.ABC bằng A.
1...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng (SBC) là 6 4 , từ B đến mặt phẳng (SAC) là 15 10 từ C đến mặt phẳng (SAB) là 30 20 và hình chiếu vuông góc của S xuống đáy nằm trong tam giác ABC. Thể tích khối chóp S.ABC bằng
A. 1 36
B. 1 48
C. 1 12
D. 1 24
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a,
S
A
⊥
(
A
B
C
)
và
S
A
a
6
. Thể tích của khối chóp S.ABC bằng: A.
a
3
2
4
B.
a
3
2
C.
a...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, S A ⊥ ( A B C ) và S A = a 6 . Thể tích của khối chóp S.ABC bằng:
A. a 3 2 4
B. a 3 2
C. a 3 3 12
D. a 3 2 12
Đáp án A
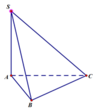
Do tam giác ABC đều cạnh a nên có S ∆ A B C = a 2 3 4
⇒ V = 1 3 S A . S ∆ A B C = 1 3 . a 6 . a 2 3 4 = a 2 2 4
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và khoảng cách từ trọng tâm tam giác ABC đến mặt bên (SAB) bằng a/4. Thể tích của hình chóp bằng:A.
3
24
a
3
B.
3
16
a
3
C.
3
12...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và khoảng cách từ trọng tâm tam giác ABC đến mặt bên (SAB) bằng a/4. Thể tích của hình chóp bằng:
A. 3 24 a 3 B. 3 16 a 3
C. 3 12 a 3 D. 2 12 a 3
Chọn A.
Gọi H là trọng tâm tam giác ABC, M là trung điểm AB, I là chân đường cao vuông góc hạ từ H đến SM. Khi đó HI = d(H,(SAB)). Từ đó tính được SH
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và thể tích của khối chóp bằng a3. Chiều cao h của hình S.ABC ứng với đỉnh S bằng bao nhiêu?
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và thể tích của khối chóp bằng a3. Chiều cao h của hình S.ABC ứng với đỉnh S bằng bao nhiêu?
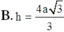
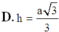
Đáp án A
Do ABC là tam giác đều cạnh a
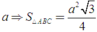
Khi đó
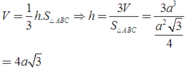
→ Đáp án A
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SBC và ABC đều là tam giác đều cạnh a. Cho SA
a
3
2
Khoảng cách từ S đến mặt phẳng (ABC) bằng: A.
a
3
3
B. a C.
3...
Đọc tiếp
Cho hình chóp S.ABC có SBC và ABC đều là tam giác đều cạnh a. Cho SA = a 3 2 Khoảng cách từ S đến mặt phẳng (ABC) bằng:
A. a 3 3
B. a
C. 3 a 4
D. a 3 2
Đáp án C
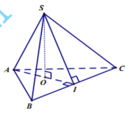
Ta chứng minh được hai mặt phẳng (SAI) (ABC) cùng vuông góc với nhau. Gọi O là hình chiếu của S lên AI
suy ra SO ⊥ (ABC)
Ta có AI =SI = a 3 2 =SA => ∆ S A I đều =>SI = SA . a 3 2 = 3 a 4
Đúng 0
Bình luận (0)