Cho hàm số y = f x . Hàm số y = f ' x có bảng biến thiên như hình vẽ dưới
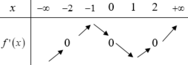
Giá trị lớn nhất của hàm số g x = f 2 x - sin 2 x trên [ -1;1]
A. f - 1
B. f 0
C. f 2
D. f 1
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng biến thiên như hình vẽ dưới đây
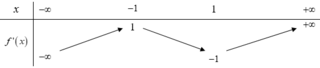
Hàm số g(x)=f(x)-x có bao nhiêu điểm cực trị?
A. 3
B. 2
C. 0
D. 1
g ' ( x ) = f ' ( x ) - 1 ; g ' ( x ) = 0 ⇔ f ' ( x ) = 1
Dựa vào bảng biến thiên của hàm số y = f ' ( x ) ta có
f ' ( x ) = 1 ⇔ [ x = - 1 x = x 0 > 1
Bảng xét dấu g ' ( x )

Vậy hàm số g(x)=f(x)-x có một điểm cực trị.
Chọn đáp án D.
Cho hàm số y=f(x). Hàm số y=f '(x) có bảng biến thiên như hình vẽ dưới
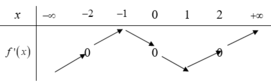
Giá trị lớn nhất của hàm số g ( x ) = f ( 2 x ) - sin 2 x trên [-1;1]
A. f(-1)
B. f(0)
C. f(2)
D. f(1)
Ta có g ( x ) = f ( 2 x ) - sin 2 x ≤ f ( 2 x ) 2 x ∈ - 2 ; 2 suy ra bảng biến thiên
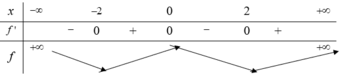
Dựa vào BBT suy ra f ( 2 x ) ≤ f ( 0 ) ⇒ g ( x ) ≤ f ( 0 ) ∀ 2 x ∈ - 2 ; 2
⇒ m a x [ - 1 ; 1 ] g ( x ) = f ( 0 ) đạt được khi
x = 0 sin 2 x = 0 ⇔ x = 0
Chọn đáp án B.
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên dưới. Hàm số y=f(x) đồng biến trên khoảng
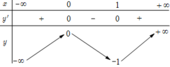
A. - 1 ; + ∞
B. 0 ; + ∞
C. 0 ; 1
D. - 3 ; - 2
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây
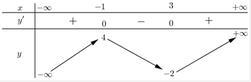
Hàm số y=f(3-x) đồng biến trên khoảng nào dưới đây ?
A. ( - ∞ ; 0 ) .
B. (4;6).
C. (-1;5).
D. (0;4).
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên dưới.
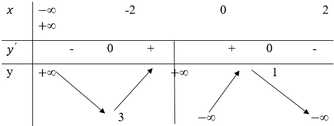
Hàm số y=f(x) đồng biến trên khoảng nào sau đây?
A. (-2;2).
B. (0;2).
C. ( 3 ; + ∞ ) .
D. ( - ∞ ; 1 ) .
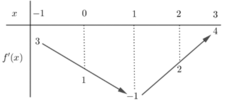
Cho hàm số y = f(x). Hàm số y’ = f’(x) có bảng biến thiên như hình vẽ bên. Hàm số g(x) = f(x) – x có bao nhiêu điểm cực trị ?
![]()
A. 3
B. 2
C. 0
D. 1
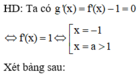
Hàm số đạt cực trị tại x = a. Chọn D.
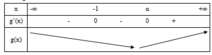
Cho hàm số y= f( x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y= f’(x) được cho như hình vẽ dưới đây.
Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng
A. (2; 4)
B. (0; 2)
C. (- 2; 0)
D.(- 4;-2)
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây
Hàm số đông biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
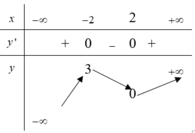
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây
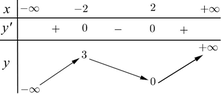
Hàm số đồng biến trên khoảng nào dưới đây ?
A. (-2;2).
B. ( - ∞ ; 3 ) .
C. ( 0 ; + ∞ ) .
D. ( 2 ; + ∞ ) .
Đáp án D
Quan sát bảng biến thiên với chiều mũi tên đi lên, hàm số đồng biến trên các khoảng ( - ∞ ; - 2 ) và ( 2 ; + ∞ ) .
Cho hàm số f(x) có bảng biến thiên như hình vẽ dưới đây
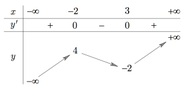
Có bao nhiêu số nguyên m để hàm số y=f(x+m) nghịch biến trên khoảng (0;1).
A. 3.
B. 5.
C. 1.
D. 4.