Gọi (H) là hình phẳng giới hạn bởi (P): y = 3 x 2 cung tròn y = 4 - x 2 ( 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ). Thể tích của khối tròn xoay thu được khi quay (H)xung quanh trục Ox bằng
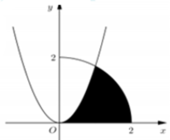
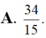
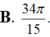
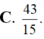
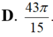
Gọi H là hình phẳng giới hạn bởi P y = 3 x 2 , cung tròn y = 4 - x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Thể tích của khối tròn xoay thu được khi quay H xung quanh trục Ox bằng
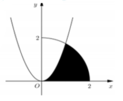
A. 34 15
B. 34 π 15
C. 43 15
D. 43 π 15
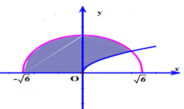
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 ( - 6 ≤ x ≤ 6 ) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
![]()
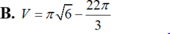
![]()
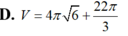
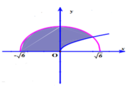
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 - 6 ≤ x ≤ 6 và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
A. V = 4 π 6 + 22 π
B. V = π 6 - 22 π 3
C. V = 8 π 6 + 11 π
D. V = 4 π 6 + 22 π 3
Chọn D.
Phương pháp: Chia miền cần tính thể tích làm 2 phần.

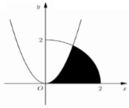
Cho (H) là hình phẳng giới hạn bởi Parabol y = 3 x 2 , cung tròn có phương trình y = 4 − x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
A. 4 π + 3 12 .
B. 4 π − 3 6 .
C. 4 π + 2 3 − 3 6 .
D. 5 3 − 2 π 3 .
Đáp án B
Xét phương trình tương giao:
3 x 2 = 4 − x 2 ⇔ 3 x 4 = 4 − x 2 ⇔ x 2 = 1 ⇒ x = ± 1 x 2 = − 4 3 ( L ) S = ∫ 0 1 3 x 2 d x + ∫ 1 2 4 − x 2 d x = 3 x 3 3 1 0 + S 2 S 2 : x = 2 sin t , t ∈ ( − π 2 ; π 2 ) ⇒ d x = 2 cos t d t S 2 : ∫ π 6 π 2 2 cos t .2 cos t d t = ∫ π 6 π 2 4 cos 2 t d t = 2 ∫ π 6 π 2 ( 1 + cos 2 t ) d t = 2 [ t + sin 2 t 2 ] π 2 π 6 = 2 π 3 − 3 2 ⇒ S = 3 3 + 2 π 3 − 3 2
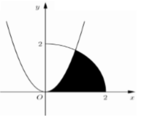
Cho (H) là hình phẳng giới hạn bởi Parabol y = 3 x 2 , cung tròn có phương trình y = 4 - x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
A. 4 π + 3 12
B. 4 π - 3 6
C. 4 π + 2 3 - 3 6
D. 5 3 - 2 π 3
Đáp án B.
Xét phương trình tương giao:
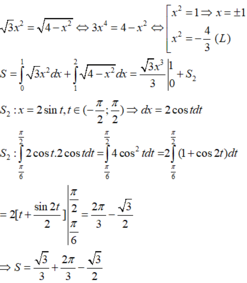
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 , cung tròn có phương trình y = 4 − x 2 (với 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ).
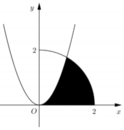
Diện tích của (H) bằng
A. 4 π + 3 12 .
B. 4 π − 3 6 .
C. 4 π + 2 3 − 3 6 .
D. 5 3 − 2 π 3 .
Đáp án B.
Phương trình hoành độ giao điểm là:
3 x 2 = 4 − x 2 ⇒ 0 ≤ x ≤ 2 3 x 4 = 4 − x 2 ⇔ x = 1.
Dựa vào hình vẽ ta có:
S = ∫ 0 1 3 x 2 d x + ∫ 1 2 4 − x 2 d x = 3 x 3 3 1 0 + I 1 = 3 3 + I 1
Với I = ∫ 1 2 4 − x 2 d x , sử dụng CASIO
hoặc đặt x = 2 sin t ⇒ d x = 2 cos t d t
Đổi cận
x = 1 ⇒ t = π 6 x = 2 ⇒ t = π 2 ⇒ I 1 = ∫ π 6 π 2 4 − 4 sin 2 t . c o s tdt = ∫ π 6 π 2 2 1 + c o s 2 t d t = 2 t − sin 2 t π 2 π 6
⇒ I 1 = 1 6 4 π − 3 3 . Do đó S = 4 π − 3 6 .
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 cung tròn có phương trình y = 4 - x 2 (với 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
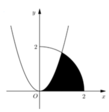
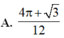
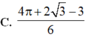
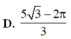
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 , cung tròn có phương trình y = 4 - x 2 (với 0 ≤ x ≤ 2 ) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 4 π + 3 12
B. 4 π - 3 6
C. 4 π + 2 3 - 3 6
D. 5 3 - 2 π 3
Phần diện tích giới hạn bởi đường x = 4 - y 2 ; x = y 3 ; y = 0; y = 3 nên diện tích cần tìm là
S = ∫ 0 3 4 - y 2 - y 3 d y rồi dùng máy tính cầm tay để kết luận.
Đáp án cần chọn là B
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = x cung tròn có phương trình y = 6 - x 2 ( 6 ≤ x ≤ 6 ) và trục hoành (phần gạch chéo trong hình vẽ). Tính thể tích V của vật thể xoay tròn sinh bởi hình phẳng D khi quay D quanh trục Ox.
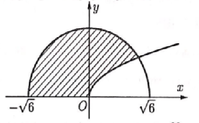
A. V = 8 π 6 - 2 π .
B. V = 8 π 6 + 22 π 3 .
C. V = 8 π 6 - 22 π 3 .
D. V = 4 π 6 + 22 π 3 .