Trong không gian Oxyz, cho 2 đường thẳng chéo nhau d : x - 3 - 4 = y + 2 1 = z + 1 1 và d ' : x - 6 = y - 1 1 = z - 2 2 . Phương trình nào dưới đây là phương trình đường thẳng vuông góc chung của d và d’
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho 2 đường thẳng chéo nhau d: d : x - 3 - 4 = y + 2 1 = z + 1 1 và d ' : x - 6 = y - 1 1 = z - 2 2 . Phương trình nào dưới đây là phương trình đường thẳng vuông góc chung của d và d’
A. x + 1 1 = y + 1 2 = z 2
B. x - 1 1 = y - 1 2 = z 2
C. x + 1 1 = y - 1 2 = z 2
D. x - 1 1 = y - 1 2 = z + 1 2
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng chéo nhau ∆ : x - 2 2 = y - 3 - 4 = z - 1 - 5 và d : x - 1 1 = y - 2 = z + 1 2 . Khoảng cách giữa hai đường thẳng ∆ và d bằng
A. 5 5
B. 45 14
C. 5
D. 3
Trong không gian Oxyz, cho hai đường thẳng chéo nhau d : x - 3 - 4 = y + 2 1 = z + 1 1 và d ' : x - 6 = y - 1 1 = z - 2 2 . Phương trình nào dưới đây là phương trình đường thẳng vuông góc chung của d và d'?
![]()
![]()
![]()

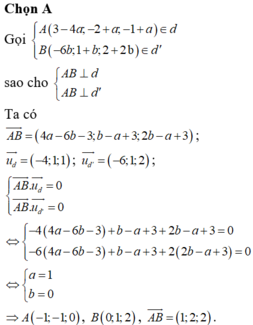
Vậy phương trình đường thẳng vuông góc chung của d và d' là ![]()
Trong không gian Oxyz, cho hai đường thẳng chéo nhau d 1 : x - 1 3 = y + 1 2 = z - 2 - 2 , d 2 : x - 4 2 = y - 4 2 = z + 3 - 1 . Phương trình đường vuông góc chung của hai đường thẳng d 1 , d 2 là
A. x - 4 2 = y + 1 - 1 = z 2
B. x - 2 6 = y - 2 3 = z + 2 - 2
C. x - 2 2 = y - 2 - 1 = z + 2 2
D. x - 4 2 = y - 1 - 1 = z 2
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau
d 1 : x = 4 - 2 t y = t z = 3 , d 2 : x = 1 y = t ' z = - t '
Phương trình mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng trên là:
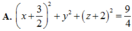

![]()
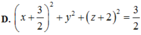
Chọn B
Đường thẳng d1 có vtcp ![]() ; đường thẳng d2 có vtcp
; đường thẳng d2 có vtcp ![]()
Giả sử M ∈ d1 => M (4 – 2t; t; 3), N ∈ d2 => N (1; t’; -t’)
Khi đó: ![]() để MN là đoạn vuông góc chung của d1 và d2 khi:
để MN là đoạn vuông góc chung của d1 và d2 khi:
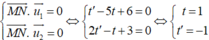
Vậy M (2; 1; 3), N (1; -1; 1)
Mặt cầu cần tìm là mặt cầu đường kính MN nên có tâm 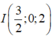 , bán kính R = MN/2 = 3/2
, bán kính R = MN/2 = 3/2
Trong không gian Oxyz cho hai đường thẳng: d 1 : x = 1 - t y = t z = - 1 d 2 : x = 2 t ' y = - 1 + t ' z = t '
Chứng minh rằng hai đường thẳng d 1 v à d 2 chéo nhau
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 3 - 1 ; d 2 : x 1 = y - 1 2 = z - 6 3 chéo nhau. Đường vuông góc chung của hai đường thẳng d 1 , d 2 có phương trình là
A. x - 1 5 = y + 2 - 4 = z - 3 1
B. x - 1 5 = y + 1 - 4 = z - 1 1
C. x + 1 5 = y + 1 - 4 = z - 3 1
D. x + 1 3 = y + 1 - 2 = z - 3 1
Đáp án C
![]()
![]()
![]()
Theo giả thiết ta giải hệ điều kiện :
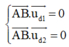
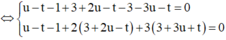
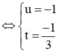
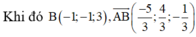
![]()
Vậy PT đường vuông góc chung là AB: x + 1 5 = y + 1 - 4 = z - 3 1
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 3 - 1 ; d 2 : x 1 = y - 1 2 = z - 6 3 chéo nhau. Đường vuông góc chung của hai đường thẳng d 1 ; d 2 có phương trình là
A. x - 1 5 = y + 2 - 4 = z - 3 1
B. x - 1 5 = y + 1 - 4 = z - 1 1
C. x + 1 5 = y + 1 - 4 = z - 3 1
D. x + 1 3 = y + 1 - 2 = z - 3 1
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau d 1 : x - 2 2 = y + 2 1 = z - 6 - 2 và d 2 : x - 4 1 = y + 2 - 2 = z + 1 3 . Phương trình mặt phẳng (P) chứa đường thẳng d1 và song song với đường thẳng d2 là
A. (P): 2x + y - 6 = 0.
B. (P): x + 8y + 5z + 16 = 0.
C. (P): x + 4y + 3z - 12 = 0.
D. (P): x + 8y + 5z - 16 = 0.