Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 1 x trên [ 1 3 ; 3 ) Tính 3M+2m
A. 13 6
B. 15
C. 14
D. 12
PB
Những câu hỏi liên quan
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
3
+
(
k
2
-
k
+
1
)
x
trên đoạn [-1;2]. Khi k thay đổi trên
ℝ
, giá trị nhỏ nhất c...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 + ( k 2 - k + 1 ) x trên đoạn [-1;2]. Khi k thay đổi trên ℝ , giá trị nhỏ nhất của M - m bằng.
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
-
1
+
2
.
cos
x
2
-
3
.
sin
x...
Đọc tiếp
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn [1;4]. Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Chọn B
Hàm số xác định và liên tục trên đoạn [1;4]. Đặt y = f(x)
Ta có: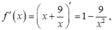 
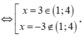
Có 
Vậy m + M = 16.
Đúng 0
Bình luận (0)
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y
x
+
9
x
trên đoạn
1
,
4
. Giá trị của m + M bằng A.
65
4
B. 16 C.
49
4
D. 10
Đọc tiếp
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn 1 , 4 . Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn [1;4]. Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + 1 x 2 + x + 1 . Giá trị của M - 3m bằng bao nhiêu?
A. 0
B. 1
C. -1
D. 2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
x
+
1
x
trên
1
3
;
3
. Tính
3
M
+
2
m
A.
3
M
+
2
m
16
3
B.
3
M
+...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 1 x trên 1 3 ; 3 . Tính 3 M + 2 m
A. 3 M + 2 m = 16 3
B. 3 M + 2 m = 15
C. 3 M + 2 m = 14
D. 3 M + 2 m = 12
Chọn C.
Phương pháp
- Tính y' và tìm nghiệm thuộc đoạn 1 3 ; 3 của y’.
- Tính giá trị của hàm số tại các điểm x = 1 3 ; x = 3 và các điểm vừa tìm được ở trên.
- So sánh các giá trị này và tìm GTLN, GTNN.
Cách giải:
Đúng 0
Bình luận (0)
Cho hàm số yf(x),
x
∈
-
2
;
3
có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn
-
2
;
3
. Giá trị của M+n là A. 6 B. 1 C. 5 D. 3
Đọc tiếp
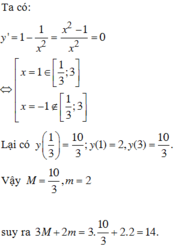
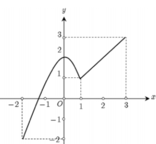
Cho hàm số y=f(x), x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn - 2 ; 3 . Giá trị của M+n là
A. 6
B. 1
C. 5
D. 3
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
y
1
−
x
−
2
x
2
x
+
1
.
Khi đó giá trị của
M
−
m
là A. –2. B. 2. C. –1. D. 1.
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = 1 − x − 2 x 2 x + 1 . Khi đó giá trị của M − m là
A. –2.
B. 2.
C. –1.
D. 1.
Đáp án B.
ĐK: 0 ≤ x ≤ 1 . Với điều kiện này ta thấy rằng tử là nghịch biên (x tăng thì giá trị tử giảm đi) còn mẫu là đồng biến và mẫu dương (x tăng thì mẫu tăng theo) vì vậy tổng thể hàm y là hàm nghịch biến. Do đó M = max x ∈ 0 ; 1 y = y 0 = 1 ; m = min x ∈ 0 ; 1 y = y 1 = − 1 vậy M − m = 2.
Đúng 0
Bình luận (0)