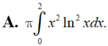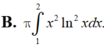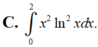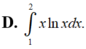Hình phẳng được giới hạn bởi các đường y = 4 − x 2 , y = 2 , y = x có diện tích là S = a + b π . Chọn kết quả đúng.
A. a > 1 , b > 1
B. a + b < 1
C. a + 2 b = 3
D. a 2 + 4 b 2 ≥ 5
Tính thể tích hình khối do hình phẳng giới hạn bởi các đường y=\(x^{\dfrac{1}{2}}e^{\dfrac{x}{2}}\) y=0,x=1,x=4
Tính thể tích hình khối do hình phẳng giới hạn bởi các đường y= \(x\sqrt{ln\left(1+x^3\right)}\) : y=0 : x=1
1.
\(V=\pi \int ^4_1[x^{\frac{1}{2}}e^{\frac{x}{2}}]^2dx=\pi \int ^4_1(xe^x)dx\)
\(=\pi \int ^4_1xd(e^x)=\pi (|^4_1xe^x-\int ^4_1e^xdx)\)
\(=\pi |^4_1(xe^x-e^x)=\pi (3e^4)=3\pi e^4\)
2.
\(V=\pi \int ^1_0(x\sqrt{\ln (x^3+1)})^2dx=\pi \int ^1_0x^2\ln (x^3+1)dx\)
\(=\frac{1}{3}\pi \int ^1_0\ln (x^3+1)d(x^3+1)\)
\(=\frac{1}{3}\pi \int ^2_1ln tdt=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1td(\ln t))\)
\(=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1dt)=\frac{1}{3}\pi |^2_1(t\ln t-t)=\frac{1}{3}\pi (2\ln 2-1)\)
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
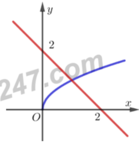
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Diện tích hình phẳng được giới hạn bởi các đường y = x 3 + 3 x , y = - x và đường thẳng x = -2 là:
A. -12(dvdt).
B. 12(dvdt).
C. 4(dvdt).\
D. -4(dvdt).
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = x3 + 3x và y = -x là: x3 + 4x = 0 ⇔ x = 0
Ta có: x3 + 4x ≤ 0, ∀ x ∈ [-2;0].
Do đó:
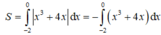
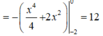
Diện tích hình phẳng được giới hạn bởi các đường y = 2 x - x 2 và đường thẳng x + y = 2 là:
A. 1 6 d v t t
B. 5 2 d v t t
C. 6 5 d v t t
D. 1 2 d v t t
Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x - x2 và x + y = 2 là :
![]()
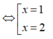
![]()
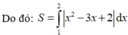
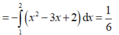
Tính diện tích hình phẳng được giới hạn bởi các đường x = y 2 ; y = x 3 ; y = x
A . 1 2
B . 1 4
C . 2 3
D . 1 3
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = 2x – x 2 , x + y = 2
Cho hình phẳng (D) giới hạn bởi các đường y = ( x - 2 ) 2 và y = 4 . Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Oy
A. 219 π 2
B. 172 π 5
C. 113 π 2
D. 128 π 3
Chọn D
D quay xung quanh trục Oy
Ta có: y = ( x - 2 ) 2 ⇔ x - 2 = ± y ⇔ x = 2 ± y
V = π ∫ 0 4 2 + y 2 - 2 - y 2 dy = 8 π . ∫ 0 4 y dy = 8 π . 2 3 y 3 2 | 0 π = 128 π 3 đ v t t
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y = xlnx; y = 0 ; x = 2 quay quanh trục Ox được tính bởi công thức nào?
A. π ∫ 0 2 x 2 ln 2 xdx
B. π ∫ 1 2 x 2 ln 2 xdx
C. ∫ 0 2 x 2 ln 2 xdx
D. ∫ 1 2 xlnxdx
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y = x ln x y = 0 ; x = 2 quay quanh trục Ox được tính bởi công thức nào?