Cho hàm số f(x) có f ' ( x ) = x 2017 ( x - 1 ) 2018 ( x + 1 ) 2018 , ∀ x ∈ ℝ . Hỏi hàm số đã cho có bao nhiêu điểm cực trị?
A. 0
B. 1
C. 2
D. 3
PB
Những câu hỏi liên quan
Cho hàm số f(x)=x-
1
x
Với x khác 0. Chứng tỏ rằng [f(2018)]2017+[f(1
2018)]2017 =0
Cho hàm số f(x) xác định trên R{1} thỏa mãn
f
(
x
)
1
x
-
1
,
f
(
0
)
2017
;
f
(
2
)
2018
. Tính S f(3)-f(-1) A. S 1 B. S ln2 C. S ln4035 D. S 4
Đọc tiếp
Cho hàm số f(x) xác định trên R\{1} thỏa mãn f ' ( x ) = 1 x - 1 , f ( 0 ) = 2017 ; f ( 2 ) = 2018 . Tính S = f(3)-f(-1)
A. S = 1
B. S = ln2
C. S = ln4035
D. S = 4
Cho hàm số yf(x) có đạo hàm cấp hai trên R. Biết f (0)3,f (2)2018 và bẳng xét dấu của f (x) như sau: Hàm số yf(x+2017)+2018x đạt giá trị nhỏ nhất tại điểm x0 thuộc khoảng nào sau đây? A. B. C. D.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm cấp hai trên R. Biết f '(0)=3,f '(2)=2018 và bẳng xét dấu của f ''(x) như sau:
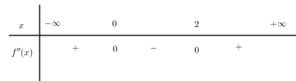
Hàm số y=f(x+2017)+2018x đạt giá trị nhỏ nhất tại điểm x0 thuộc khoảng nào sau đây?
A.
B.
C.
D.
Cho f(x)
x
x
2
+
1
(
2
x
2
+
1
+
2017
)
, biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)2018. Tính F(2) A. F(2) 5+2017
5
B. F(2) 4+2017
4
C. F(2) 3+2017
3...
Đọc tiếp
Cho f(x)= x x 2 + 1 ( 2 x 2 + 1 + 2017 ) , biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)=2018. Tính F(2)
A. F(2) = 5+2017 5
B. F(2) = 4+2017 4
C. F(2) = 3+2017 3
D. F(2)= 2022
cho hàm số f(x)=ax2+bx+c ( x là ẩn , a,b,c là hệ số ) . Biết rằng f(0)=2018, f(1)=2019,f(-1)=2017 . Tính f(-2019)
Cho hàm số f(x) có đạo hàm trên
ℝ
thỏa mãn f’(x) – 2018f(x) 2018.x2017.e2018x với mọi
x
∈
ℝ
và f(0) 2018. Tính giá trị f(1). A. f(1) 2019e2018. B. f(1) 2018e-2018. C. f(1) 2018e2018. D. f(1) 2017e2018.
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên ℝ thỏa mãn f’(x) – 2018f(x) = 2018.x2017.e2018x với mọi x ∈ ℝ và f(0) = 2018. Tính giá trị f(1).
A. f(1) = 2019e2018.
B. f(1) = 2018e-2018.
C. f(1) = 2018e2018.
D. f(1) = 2017e2018.
Chọn A
Lấy tích phân từ 0 đến 1 của 2 vế:
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)0 và thỏa mãn
f
(
x
)
2018
1
-
f
(
x
)
2
x
(...
Đọc tiếp
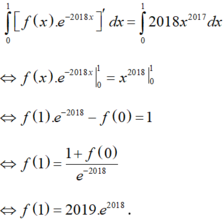
Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x ) = 2 x ( x + 1 ) 2 ( x - 2018 ) 2019 : f ' ' ( x ) , ∀ x ∈ R Hàm số g ( x ) = f ' ( x ) 2019 1 - f ' ' ( x ) có bao nhiêu điểm cực trị?
A. 1
B.2
C.3
D. 4
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = - 2017 ( x - 1 ) ( x + 2 ) 3 ( x - 3 ) 2 Tìm số điểm cực trị của f(x)
A. 3
B. 2
C. 0
D. 1
Đáp án B
Ta có y , = 0 ⇔ x = 1 x = - 2 x = 3 , y , đổi dấu qua x=1 và x=-2 , y , không đổi dấu qua x=3 nên hàm số có hai cực trị tại x=1 và x=-2
Đúng 0
Bình luận (0)
Cho hàm số y f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) (1–x)(x+2)g(x)+2018 với g(x) 0,
∀
x
∈
R
. Hàm số y f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào? A.
1
;
+
∞
B.
0
;...
Đọc tiếp
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra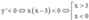 
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
Đúng 0
Bình luận (0)