Giả sử phương trình z 2 + z + 2 2018 = 0 có hai nghiệm phân biệt z 1 , z 2 . Tính giá trị của biểu thức P = log 2 z 1 2018 + log 2 z 2 2018 .
A. 1 2 1009 .
B. 2 1009 .
C. 2018 2 .
D. 4036
Cho hệ phương trình - x + 2 y - 3 z = 2 6 x - y + 3 z = - 3 - 2 x - 3 y + z = 2
Giả sử (x; y;z) là nghiệm của hệ phương trình. Trong các khẳng định sau, khẳng định đúng là
![]()
![]()
![]()
![]()
Cho hệ phương trình 2 x - 3 y + 4 z = - 5 - 4 x + 5 y - z = 6 3 x + 4 y - 3 z = 7 . Giả sử (x;y;z) là nghiệm của hệ phương trình, khi đó x+y+z bằng
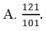
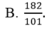
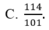
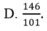
Tại sao khi một phương trình có vai trò các ẩn bình đẳng nhau chẳng hạn :\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=2\) thì ta có thể giả sử \(x\le y\le z\)
để tìm ẩn. Chứ phương trình bình thường thì không được hay sao?
1.cho x thuộc Z, chứng minh rằng x^200+x^100+1 chia het cho x^4+x^2+1
2.tìm các số tự nhiênx,y,z thỏa mãn phương trình:2016^x+2017^y=2018^z
Cho hệ phương trình 0 , 5 x - 0 , 5 y + 4 z = 4 0 , 75 x + 0 , 75 y - 3 z = - 9 0 , 2 x - 0 , 14 y - 7 z = 1
Giả sử (x; y ; z) là nghiệm của hệ phương trình. Trong các khẳng định sau, khẳng định sai là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz , cho ba mặt cầu lần lượt có phương trình là ( x + 5 ) 2 + ( y - 1 ) 2 + z 2 = 5 ; x 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 6 và ( x + 1 ) 2 + y 2 + ( z - 4 ) 2 = 9 . Gọi M là điểm di động ở ngoài ba mặt cầu và X, Y , Z là các tiếp điểm của các tiếp tuyến vẽ từ M đến ba mặt cầu. Giả sử MX = MY = MZ , khi đó tập hợp các điểm M là đường thẳng có vectơ chỉ phương là
![]()
![]()
![]()
![]()
xyz/x+y=2
xyz/y+z=1,2
xyz/x+z=1,5
Giả hệ phương trình trên
Bài 1: Cho hệ phương trình: \(\hept{\begin{cases}x+y=2a-1\\x^2+y^2=a^2+2a-3\end{cases}}\)
Giả sử (x; y) là nghiệm của hệ phương trình. Xác định a để xy đạt GTNN. Tìm GTNN đó.
Bài 2: Giải hệ phương trình: \(\hept{\begin{cases}\left(c+a\right)y+\left(a+b\right)z-\left(b+c\right)x=2a^3\\\left(a+b\right)z+\left(b+c\right)x-\left(c+a\right)y=2b^3\\\left(b+c\right)x+\left(c+a\right)y-\left(a+b\right)z=2c^3\end{cases}}\)
Đặt S=x+y, P=x.y
Ta có:S=2a-1, x^2+y^2=S^2-2P=a^2+2a-3
\Rightarrow P=\frac{1}{2}[(2a-1)^2-(a^2+2a-3)]=\frac{1}{2}(3a^2-6a+4)
Trước hết tìm a để hệ có nghiệm.
Điều kiện để hệ có nghiệm:S^2-4P \geq 0 \Leftrightarrow (2a-1)^2-2(3a^2-6a+4)\geq 0
\Leftrightarrow -2a^2+8a-7 \geq 0 \leftrightarrow 2-\frac{\sqrt{2}}{2} \leq a \leq 2+\frac{\sqrt{2}}{2} (1)
Tìm a để P=\frac{1}{2}(3a^2-6a+4) đạt giá trị nhỏ nhất trên đoạn
[2-\frac{\sqrt{2}}{2} ;2+\frac{\sqrt{2}}{2}]
Ta có hoành độ đỉnh a_0=\frac{6}{2.3}=1Parabol có bề lõm quay lên do đó \min P=P(2-\frac{\sqrt{2}}{2} )$
Vậy với a=2-\frac{\sqrt{2}}{2} thì xy đạt giá trị nhỏ nhất.
1)cho 3 số x, y,z thỏa mãn điều kiện x+y+z=2018 và x^3+y^3+z^3=2018^3. Cmr (x+y+z)^3=x^2017+y^2017+z^2017
2)
tìm các cặp số nguyên (x y) biết x^2-4xy+5y^2-16=0
3)Cho 3 số a,b,c thỏa mãn a+b+c=0 và a^2+b^2+c^2=2018
4)tính giả trị biểu thức A=a^4+b^4+c^4