Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + 6 x + 5 m nghịch biến trên khoảng 10 ; + ∞
A. 5
B. 3
C. 4
D. Vô số
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + 6 x + 5 m nghịch biến trên khoảng 10 ; + ∞
A. 5.
B. 3.
C. 4.
D. Vô số.
Đáp án C
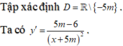
Để hàm số nghịch biến trên khoảng ( 10 ; + ∞ ) thì
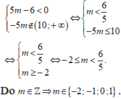
Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:
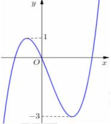
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
Có tất cả bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số y = x 3 - x 2 + ( m 2 + 1 ) x - 4 m - 7 trên đoạn [ 0; 2]m không vượt quá 15 ?
A. 4
B . 6
C. 5
D. 8
+ Xét hàm số f( x) = x3- x2+ ( m2+ 1) x- 4m- 7 trên đoạn [ 0; 2]
Ta có f’ (x) = 3x2- 2x+ m2+ 1= 3( x-1/3) 2+ m2+ 2/3> 0 .
+ Suy ra hàm số f(x) đồng biến trên
0 ; 2 ⇒ m i n [ 0 ; 2 ] f ( x ) = f ( 0 ) = - 4 m - 7 m a x [ 0 ; 2 ] f ( x ) = f ( 2 ) = 2 m 2 - 4 m - 1
+ Khi đó
m a x [ 0 ; 2 ] y = m a x [ 0 ; 2 ] f ( x ) = m a x - 4 m - 7 ; 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 4 m - 7 ≤ 15 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 11 2 ≤ m ≤ 2 2 m 2 - 4 m - 16 ≤ 0 ⇔ - 11 2 ≤ m ≤ 2 - 2 ≤ m ≤ 4 ⇔ - 2 ≤ m ≤ 2 → m ∈ ℤ m ∈ ± 2 ; ± 1 ; 0
Vậy có 5 giá trị thoả mãn.
Chọn C.
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số ![]() có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
A. 1
B. 0
C. 2
D. 4
Có bao nhiêu giá trị m nguyên để hàm số y = 2 x 2 + m x + 2 3 2 xác định với mọi x ∈ R ?
A. 5
B. 4
C. 7
D. 9
Tìm tất cả các giá trị thực của tham số m để hàm số y = log 2 log 5 m - 2 2 + 2 m - 3 x + m có tập xác định là ℝ.
A. m≤ 7/3.
B. m >7/3.
C. m ≥7/3.
D. m< 7/3.
Có bao nhiêu giá trị m nguyên để hàm số f ( x ) = 2 x 2 + m x + 2 3 2 xác định với mọi x ∈ R
A. 5
B. 4.
C. 7
D. 9
Có bao nhiêu giá trị m nguyên để hàm số f(x) = 2 x 2 + m x + 2 3 2 xác định với mọi x ∈ ℝ ?
A. 5
B. 4
C. 7
D. 9
Chọn C
Hàm số f(x) =
2
x
2
+
m
x
+
2
3
2
xác định với mọi
x
∈
ℝ
![]()
![]()
Vì m nguyên nên ![]()
Vậy có tất cả 7 giá trị m thỏa mãn điều kiện đề bài.
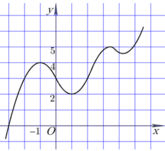
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình
f
(
x
2
-
2
x
)
=
m
có đúng 4 nghiệm thực phân biệt thuộc đoạn
[
-
3
2
;
7
2
]
.
A. 1
B. 4
C. 2
D. 3