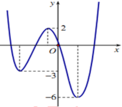
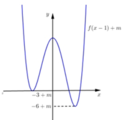
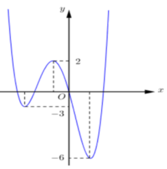
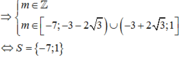Gọi S là tập tất cả giá trị của tham số m để đồ thị hàm số
y
x
4
-
2
m
+
1
x
2
+
m
có ba điểm cực trị A, B, C sao cho OABC ; trong đó O là gốc tọa độ, A là điểm cực trị trên trục tung và B, C là hai điểm cực trị còn lại. Tích của tất cả các phần tử trong tập S bằng A. 8 B. -8 C. 4 C. -4
Đọc tiếp
Gọi S là tập tất cả giá trị của tham số m để đồ thị hàm số
y
=
x
4
-
2
m
+
1
x
2
+
m
có ba điểm cực trị A, B, C sao cho OA=BC ; trong đó O là gốc tọa độ, A là điểm cực trị trên trục tung và B, C là hai điểm cực trị còn lại. Tích của tất cả các phần tử trong tập S bằng
A. 8
B. -8
C. 4
C. -4