Tìm m ∈ ℝ để phương trình 9 x - m + 1 . 3 x + m + 9 = 0 có nghiệm
![]()
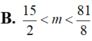
![]()
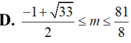
Cho bất phương trình 2 − x 2 + 2 x + 1 + 2 x 2 − 2 x ≥ m . Tìm m để bất phương trình đúng với mọi x ∈ ℝ
A. m ≤ 3
B. m ≥ 3 2
C. m ≤ 2 2
D. m ≤ 3 2
Đáp án C
Đặt t = 2 x 2 − 2 x , t ∈ 0 ; + ∞ ⇒ B P T ⇔ 2 t + t ≥ m 1
Ta có t + 2 t ≥ 2 t . 2 t = 2 2 ⇒ 1 ⇔ m ≤ 2 2
Tìm m để bất phương trình 2 cos 2 x + 3 sin 2 x ≥ m . 3 cos 2 x nghiệm đúng ∀ x ∈ ℝ
A. m ≤ 0
B. m ≤ 1
C. m ≤ 4
D. m ≤ - 1
Tìm m để các bất phương trình 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 ≤ m + 1 đúng với mọi x ∈ ℝ
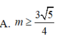
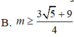
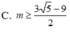
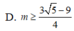
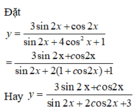
(Do sin 2x + 2cos2x + 3> 0 với mọi x nên hàm số xác định trên R)
Khi đó, ta có: y. (sin 2x+ 2cos 2x+ 3) = 3sin2x + cos2x
ó ( 3- y)sin2x + (1- 2y).cos2x = 3y
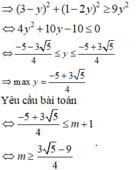
Đáp án D
Tìm các giá trị m ∈ ℝ để phương trình 5 x 2 + m x - 2 - 5 2 x 2 - m x - m + 2 = x - m x - m có nghiệm x ∈ 0 ; 1 .
A. - 1 ≤ m ≤ 0
B. 0 ≤ m ≤ 1 3
C. m ≤ - 1 hoặc m ≥ 0
D. - 3 ≤ m ≤ - 1
Tìm m để bất phương trình sau luôn đúng với mọi x
x + m x 2 + x + 1 ≤ 1 ∀ x ∈ ℝ
A. m ≥ 0
B.m ≤ 1
C. 0 ≤ m ≤ 1
D.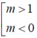
Chọn C
Ta có: x2+ x+ 1> 0 với mọi x
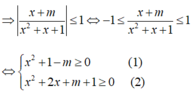
Để bất phương trình đã cho luôn đúng với mọi x khi và chỉ khi (1) và (2) luôn đúng với x
+ (1) đúng với mọi x khi và chỉ khi 1-m≥0 hay m≤ 1
+ (2) đúng với mọi x khi và chỉ khi ∆’ =- m ≤ 0 hay m≥ 0
Vậy 0≤ m≤ 1 là những giá trị cần tìm
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 3 x + m - 1 3 x + m - 1 > 0 nghiệm đúng ∀ x ∈ ℝ .
A . m ∈ R
B . m > 1
C . m ≤ 1
D . m ≥ 1
Tìm m ∈ ℝ để phương trình 2 sin 2 x + 3 cos 2 x = m . 3 sin 2 2 x có nghiệm.
A. 1 ≤ m ≤ 4
B. 2 ≤ m ≤ 3
C. 1 ≤ m ≤ 3
D. 2 ≤ m ≤ 4
Tìm tất cả các giá trị của m để bất phương trình 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 ≤ m + 1 đúng với mọi x ∈ ℝ
A. m ≥ 3 5 4
B. m ≥ 3 5 + 9 4
C. m ≥ 65 − 9 2
D. m ≥ 65 − 9 4
Đáp án D
Ta có : y = 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
và sin 2 x + 2 cos 2 x + 3 > 0 ; ∀ x ∈ ℝ
xét phương trình
y = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
⇔ sin 2 x + 2 cos 2 x + 3 y = 3 sin 2 x + cos 2 x ⇔ y − 3 sin 2 x + 2 y − 1 cos 2 x = − 3 y
Phương trình trên có nghiệm nên
y − 3 2 + 2 y − 1 2 ≥ − 3 y 2 ⇔ 5 y 2 − 10 y + 10 ≥ 9 y 2
⇔ − 4 y 2 − 10 y + 10 ≥ 0 ⇔ − 5 − 65 4 ≤ y ≤ − 5 + 65 4
Suy ra giá trị lớn nhất của y là − 5 + 65 4
Phương trình 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3 ≤ m + 1 nghiệm đúngg với mọi số thực x khi
− 5 + 65 4 ≤ m + 1 ⇔ m ≥ − 9 + 65 4
Tìm tất cả các giá trị của m để bất phương trình 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 ≤ m + 1 đúng với mọi x ∈ ℝ
A. m ≥ 3 5 4
B. m ≥ 3 5 + 9 4
C. m ≥ 65 − 9 2
D. m ≥ 65 − 9 4
Đáp án D
Ta có :
y = 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
Và sin 2 x + 2 cos 2 x + 3 > 0 ; ∀ x ∈ ℝ .
xét phương trình y = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
⇔ sin 2 x + 2 cos 2 x + 3 y = 3 sin 2 x + cos 2 x ⇔ y − 3 sin 2 x + 2 y − 1 cos 2 x = − 3 y
Phương trình trên có nghiệm nên
y − 3 2 + 2 y − 1 2 ≥ − 3 y 2 ⇔ 5 y 2 − 10 y + 10 ≥ 9 y 2
⇔ − 4 y 2 − 10 y + 10 ≥ 0 ⇔ − 5 − 65 4 ≤ y ≤ − 5 + 65 4
Suy ra giá trị lớn nhất của y là − 5 + 65 4
Phương trình 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3 ≤ m + 1 nghiệm đúngg với mọi số thực x khi − 5 + 65 4 ≤ m + 1 ⇔ m ≥ − 9 + 65 4