Cho hai số thực dương a,b thoả mãn a+b=2018 và ∫ a b x x + 2018 - x d x = 10 . Tích phân ∫ a b s i n ( π x 3 ) d x bằng
A. 3 3 2 π
B. - 3 3 2 π
C. 9 2 π
D. - 9 2 π
Cho hai số thực dương a,b thoả mãn a+b = 2018 và ∫ a b x x + 2018 - x d x = 10 Tích phân ∫ a b sin πx 3 d x bằng
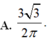
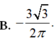
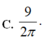
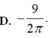
Cho hai số thực dương a,b thoả mãn a + b = 2018 và ∫ a b x x + 2018 - x d x = 10 Tích phân ∫ a b sin π x 3 d x bằng
A. 3 3 2 π
B. - 3 3 2 π
C. 9 2 π
D. - 9 2 π
cho các số a,b,x,y thoả mãn a+b=x+y và a^4+b^4=x^2+y^2.Cm a^2018+b^2018=x^2018+y^2018
Giúp mk nha mn
Dạng bài tập chứng minh dạng tổng quát rồi suy ra đpcm
Bài làm :
Xét dạng tổng quát : Cho \(\hept{\begin{cases}a+b=x+y\\a^4+b^4=x^4+y^4\end{cases}}\)
\(a^k+b^k=x^k+y^k\)(1)
+) Xét \(k=1\)ta có (1) hiển nhiên đúng
+) Xét \(k=2\)ta cũng thu được (1) đúng
Giả sử (1) đúng với \(k=n\)
Ta cần chứng minh (1) đúng với \(k=n+1\)
Khi đó : \(\left(1\right)\Leftrightarrow a^{n+1}+b^{n+1}=x^{n+1}+y^{n+1}\)
Xét \(a^{n+1}+b^{n+1}=\left(a^n+b^n\right)\left(a+b\right)-a^nb-ab^n\)
\(=\left(a^n+b^n\right)\left(a+b\right)-ab\left(a^{n-1}+b^{n-1}\right)\)
\(=\left(x^n+y^n\right)\left(x+y\right)-ab\left(x^{n-1}+y^{n-1}\right)\)(*)
Ta có \(x^2+y^2=a^2+b^2\Leftrightarrow\left(x+y\right)^2-2xy=\left(a+b\right)^2-2ab\)
\(\Leftrightarrow-2xy=-2ab\Leftrightarrow xy=ab\)
Khi đó : (*)\(\Leftrightarrow\left(x^n+y^n\right)\left(x+y\right)-xy\left(x^{n-1}+y^{n-1}\right)=x^{n+1}+y^{n+1}\)
Ta có đpcm
Xem thêm : Câu hỏi của Nguyễn Thu Huyền - Toán lớp 8 | Học trực tuyến

cho 3 số thực a,b,c thoả mãn x+y+z=9 và x^2+y^2+z^2=27 tính (x-4)^2018+(y-4)2019+(z-4)^2020
\(x+y+z=9\Leftrightarrow\left(x+y+z\right)^2=81\\ \Leftrightarrow x^2+y^2+z^2+2\left(xy+yz+xz\right)=81\\ \Leftrightarrow xy+yz+xz=\dfrac{81-27}{2}=27\\ \Leftrightarrow x^2+y^2+z^2=xy+yz+xz\\ \Leftrightarrow2x^2+2y^2+2z^2=2xy+2yz+2xz\\ \Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2xz+x^2\right)=0\\ \Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=0\\y-z=0\\z-x=0\end{matrix}\right.\Leftrightarrow x=y=z=\dfrac{9}{3}=3\left(x+y+z=9\right)\)
\(\Leftrightarrow\left(x-4\right)^{2018}+\left(y-4\right)^{2019}+\left(z-4\right)^{2020}\\ =\left(-1\right)^{2018}+\left(-1\right)^{2019}+\left(-1\right)^{2020}=1-1+1=1\)
Cho a,b,c là những số thực dương thoả mãn a < b < c < d. Xác định tập hợp X = (a;b) \(\cap\)(c;d)
A. X = ∅
B. X = (a:d)
C. X = {a; b; c; d}
D. X = (b;c)
23. Cho hs y= f(x) có đạo hàm f'(x) =-x^2-1 . Với các số thực dương a,b thoả mãn a
Ai giải giúp mk với bt khó v :<
À mà chỉ giải bằng bđt AM-GM nhé, nếu có thêm bổ đề thì chứng minh chi tiết hộ mk :)
1. Cho ba số thực dương a,b,c thoả mãn a+b+c=3
CMR : \(a.\sqrt[3]{3-b+c}+b.\sqrt[3]{3-c+a}+c.\sqrt[3]{3-a+b}\le3.\sqrt[3]{3}\)
2. Cho 3 số thực dương a,b,c thoả mãn abc=2
CMR: \(a^3+b^3+c^3\ge a\sqrt{b+c}+b\sqrt{c+a}+c\sqrt{a+b}\)
3. Cho 2 số thực dương x,y thoả mãn x+y+xy=3
CMR: \(\sqrt{\frac{x^2}{x^2+3}}+\sqrt{\frac{y^2}{y^2+3}}\le1\)
Cho các số thực dương a,b, x thoả mãn log 1 2 x = 2 3 log 1 2 a - 1 5 log 1 2 b . Mệnh đề nào dưới đây đúng ?
A. x = a 2 3 b 1 5
B. x = 2 3 a - 1 5 b
C. x = a 2 3 b - 1 5
D. x = a 3 2 b - 5
Cho các số thực dương a,b, x thoả mãn log 1 / 2 x = 2 3 log 1 / 2 a - 1 5 log 1 / 2 b . Mệnh đề nào dưới đây đúng ?
A.![]()
B. ![]()
C. ![]()
D. ![]()