Trong không gian Oxyz phương trình mặt phẳng Oxz là
A. x = y
B. y = z
C. z = 0
D. y = 0
Trong không gian Oxyz, cho hình lập phương ABCD.A’B’C’D’ sao cho A ( 0;0;0 ); B( a;0;0 ); D ( 0;a;0 ); A' ( 0;0;a ). Xét các mệnh đề sau:(I): x + y + z - a = 0 là phương trình mặt phẳng (A’BD). (II): x + y + z - 2a = 0 là phương trình mặt phẳng (CB’D). Hãy chọn mệnh đề đúng.
A. Chỉ (I)
B. Chỉ (II)
C. Cả hai đều sai
D. Cả hai đều đúng
Thay các tọa độ B( a;0;0 ); D ( 0;a;0 ); A' ( 0;0;a ) vào phương trình ( I ) thấy thỏa mãn nên ( I ) đúng
Đáp án D
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : x + y - z - 2 = 0 và đường thẳng d : x + 1 2 = y - 1 1 = z - 2 1 Phương trình nào dưới đây là phương trình mặt phẳng chứa đường thẳng (d) và vuông góc với mặt phẳng α
A. x+y-z+2=0
B. 2x-3y-z+7=0
C. x+y+2z-4=0
D. 2x-3y-z-7=0
Đáp án B
Phương pháp giải:
Ứng dụng của tích có hướng để tìm vectơ pháp tuyến của mặt phẳng. Phương trình mặt phẳng đi qua M ( x 0 ; y 0 ; z 0 ) và có VTPT
![]()
![]()
Lời giải:
![]()
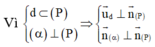
![]()
![]()
Vậy phương trình mặt phẳng (P): 2x-3y-z+7=0
Trong không gian Oxyz cho mặt phẳng (P): x + y + z - 3 = 0 và đường thẳng d : x 1 = y + 2 2 = z - 2 1 . Hình chiếu vuông góc của d trên mặt phẳng (P) có phương trình là
A. x + 1 - 1 = y + 1 - 4 = z + 1 5
B. x - 1 3 = y - 1 - 2 = z - 1 - 1
C. x - 1 1 = y - 1 4 = z - 1 - 5
D. x - 1 1 = y - 4 1 = z + 5 1
Trong không gian Oxyz, cho mặt phẳng ( P ) : x + y + z - 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z - 2 - 1 . Đường thẳng d’ đối xứng với d qua mặt phẳng (P) có phương trình là
A. x - 1 1 = y - 1 - 2 = z - 1 7
B. x - 1 1 = y - 1 2 = z + 1 - 7
C. x - 1 1 = y + 1 - 2 = z + 1 7
D. x + 1 - 1 = y - 1 2 = z - 1 - 7
Trong không gian Oxyz, cho mặt phẳng (P): x + y + z - 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z - 2 - 1 . Đường thẳng d' đối xứng với d qua mặt phẳng (P) có phương trình là
![]()
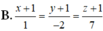
![]()
![]()
Trong không gian Oxyz, cho đường thẳng d : x - 1 2 = y - 2 1 = z + 1 3 và mặt phẳng (P): x+y+z−3=0. Đường thẳng là hình chiếu của d lên mặt phẳng (P) theo phương Ox có phương trình là
A. x - 2 2 = y - 2 - 1 = z + 1 - 1
B. x - 2 4 = y - 2 - 1 = z + 1 - 3
C. x + 2 2 = y + 2 - 1 = z - 1 - 1
D. x + 2 4 = y + 2 - 1 = z - 1 - 3
Trong không gian Oxyz, cho đường thẳng d : x - 1 1 = y - 2 2 = z - 3 1 và mặt phẳng ( α ) : x + y + z - 2 = 0 Đường thẳng nằm trong mặt phẳng ( α ) , đồng thời vuông góc và cắt đườn thẳng d có phương trình là
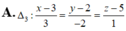
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z-7=0 và đường thẳng d : x - 3 - 2 = y + 8 4 = z - 1 . Phương trình mặt phẳng (Q) chứa d đồng thời vuông góc với mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, mặt phẳng qua A(1;2;-1) và vuông góc với các mặt phẳng (P): 2x-y+3z-2=0 (Q): x+y+z-1=0 có phương trình là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P = x + y + z − 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z − 2 − 1 . Đường thẳng d ' đối xứng với d qua mặt phẳng (P) có phương trình là
A. x + 1 1 = y + 1 2 = z + 1 7
B. x + 1 1 = y + 1 − 2 = z + 1 7
C. x − 1 1 = y − 1 2 = z − 1 7
D. x − 1 1 = y − 1 − 2 = z − 1 7