Có bao nhiêu giá trị nguyên âm của a để đồ thị hàm số y = x 3 + a + 10 x 2 - x + 1 cắt trục hoành tại đúng một điểm?
A. 9
B. 8
C. 11
D. 10
Có bao nhiêu giá trị nguyên âm của a để đồ thị hàm số y = x 3 + ( a + 10 ) x 2 - x + 1 cắt trục hoành tại đúng 1 điểm
A. 8
B. 11
C. 9
D. 10
Có bao nhiêu giá trị nguyên âm của a để đồ thị hàm số y = x 3 + a + 10 x 2 − x + 1 cắt trục hoành tại đúng một điểm?
A. 9
B. 8
C. 11
D. 10
Đáp án D.
Phương trình hoành độ giao điểm của (C) và Ox là x 3 + a + 10 x 2 − x + 1 = 0 (*).
Dễ thấy x = 0 không là nghiệm của phương trình (*). Khi đó (*) ⇔ − a − 10 = x 3 − x + 1 x 2 .
Xét hàm số f x = x 3 − x + 1 x 2 = x − 1 x + 1 x 2 , có f ' x = x 3 + − 2 x 3 = 0 ⇔ x = 1.
Tính:
lim x → − ∞ x = − ∞ ; lim x → + ∞ x = + ∞ ; lim x → 0 − x = + ∞ ; lim x → 0 + x = − ∞ ; f 1 = 1.
Dựa vào bảng biến thiên, ta thấy f x = − a − 10 có nghiệm duy nhất ⇔ a > − 11.
Kết hợp với a là số nguyên âm ⇒ Có 10 giá trị cần tìm.
Có bao nhiêu giá trị nguyên âm của a để đồ thị hàm số y = x 3 + a + 10 x 2 − x + 1 cắt trục hoành tại đúng một điểm?
A. 9
B. 8
C. 11
D. 10
Có bao nhiêu giá trị nguyên âm của m để đồ thị hàm số y = x 3 − 3 x 2 + 1 − m x + m + 1 cắt Ox tại 3 điểm phân biệt
A. 1
B. 2
C. 3
D. 4
Có bao nhiêu giá trị nguyên âm của m để đồ thị hàm số y = x 3 − 3 x 2 + 1 − m x + m + 1 cắt Ox tại 3 điểm phân biệt.
A. 1
B. 2
C. 3.
D. 4
Đáp án A
Xét phương trình hoành độ giao điểm:
x 3 − 3 x 2 + 1 − m x + m + 1 = 0
⇔ x − 1 x 2 − 2 x − m − 1 = 0 ⇔ x = 1 g x = x 2 − 2 x − m − 1 = 0
Yêu cầu bài toán ⇔ g x = 0 có 2 nghiệm phân biệt
⇔ Δ g x > 0 g x ≠ 0 ⇔ m > − 2
=>Có 1 giá trị m thỏa mãn
Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 100 ) + m 2 có 5 điểm cực trị?

A. 0.
B. 1.
C. 2.
D. 4.
Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f x + 100 + m 2 có 5 điểm cực trị?
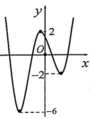
A. 0
B. 1
C. 2
D. 4
Chọn đáp án C
Hàm số y=f(x+100) có đồ thị là đồ thị hàm số y=f(x) tịnh tiến sang trái 100 đơn vị
Dựa vào đồ thị ta thấy đồ thị hàm số y=f(x) có 3 điểm cực trị.
Khi tịnh tiến sang trái 100 đơn vị thì số điểm cực trị hàm số y=f(x+100) vẫn là 3 điểm cực trị.

Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f ( x ) + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tính tổng T = a + b.
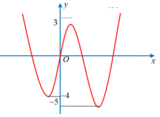
A. T = 2
B. T = 1
C. T = -1
D. T = -2
Đáp án A
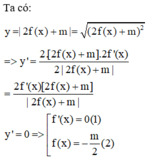
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
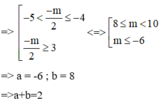
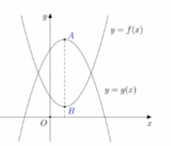
Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là A, đồ thị hàm số y = g(x) có đúng một điểm cực trị là B và A B = 7 4 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số y = f ( x ) - g ( x ) + m có đúng 5 điểm cực trị?
A. 1
B. 3
C. 4
D. 6