Tính đường kính mặt cầu ngoại tiếp hình lập phương có cạnh bằng a 3 .
![]()
![]()
![]()
![]()
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho lăng trụ đứng ABC.A’B’C’ có AB = AC = a, B C = a 3 . Cạnh bên AA' = 2a. Bán kính mặt cầu ngoại tiếp tứ diện AB’C’C bằng
A. a
B. a 5
C. a 3
D. a 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
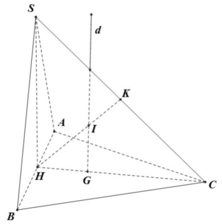
A. 5 π 15 18
B. 5 π 15 54
C. 4 π 3 27
D. 5 π 3
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
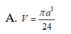
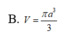
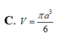
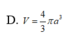
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
A. V = πa 3 24
B. V = πa 3 3
C. V = πa 3 6
D. V = 4 3 πa 3
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a;AD=2a và AA'=3a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ACB’D’.
A. a 3 2
B. a 14 2
C. a 6 2
D. a 3 4
Cho hình chóp đều n cạnh (n ≥ 3). Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng 60 ∘ , thể tích khối chóp bằng 3 3 4 R 2 . Tìm n?
A. n = 4
B. n = 8
C. n = 10
D. n = 6
Cho hình chóp đều n cạnh n ≥ 3 . Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng 60 ° , thể tích khối chóp bằng 3 3 4 . R 3 . Tìm n?
A. n = 4
B. n = 8
C. n = 10
D. n = 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C với CA=CB=a;SA=a 3 ; SB=a 5 và SC=a 2 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC?
A. a 11 6
B. a 11 2
C. a 11 3
D. a 11 4
Cho tứ diện ABCD có (ACD) vuông (BCD), tam giác ACD đều cạnh 2a, tam giác BCD cân tại B có BC=acan5. Tìm tâm bán kính mặt cầu ngoại tiếp
p/s ve hình hộ mk vs
Gọi H là trung điểm của BC.
Ta có tam giác ABC đều nên AH⊥ (BCD) , mà (ABC) ⊥ (BCD) → AH ⊥ (BCD).
Ta có AH⊥ HD→AH = AD.tan600 =a3√ & HD = AD.cot600 =a3√3
ΔBCD→BC = 2HD = 2a3√3suy ra V=13SBCD.AH=13.12BC.HD.AH=a33√9
Gọi H là trung điểm của BC.
Ta có tam giác ABC đều nên AH⊥ (BCD) , mà (ABC) ⊥ (BCD) → AH ⊥ (BCD).
Ta có AH⊥ HD→AH = AD.tan600 =a3√ & HD = AD.cot600 =a3√3
ΔBCD→BC = 2HD = 2a3√3suy ra V=13SBCD.AH=13.12BC.HD.AH=a33√9
Gọi H là trung điểm của BC.
Ta có tam giác ABC đều nên AH⊥ (BCD) , mà (ABC) ⊥ (BCD) → AH ⊥ (BCD).
Ta có AH⊥ HD→AH = AD.tan600 =a3√ & HD = AD.cot600 =a3√3
ΔBCD→BC = 2HD = 2a3√3suy ra V=13SBCD.AH=13.12BC.HD.AH=a33√9