Trong không gian tọa độ Oxyz cho đường thẳng △ có phương trình x - 1 2 = y + 1 - 1 = z 2 và mặt phẳng ( α ) có phương trình x+y-z-2=0 Tính côsin của góc tạo bởi đường thẳng △ và mặt phẳng ( α )
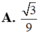
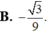
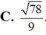
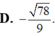
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = - 3 t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = 3 - t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Trong không gian tọa độ Oxyz, cho đường thẳng (D) có phương trình x - x o a = y - y o b = z - z o c . Đường thẳng (D) có
A. 1 vec-tơ chỉ phương
B. 2 vec-tơ chỉ phương.
C. 3 vec-tơ chỉ phương
D. vô số vec-tơ chỉ phương
Chọn đáp án D
Đường thẳng (D) có một vec-tơ chỉ phương là u 1 ⇀ = a , b , c .
Suy ra tất cả các vec-tơ u ⇀ = k u 1 ⇀ = k a ; k b ; k c k ≠ 0 ; k ∈ R cùng phương với vec-tơ u 1 ⇀ đều là vec-tơ chỉ phương của đường thẳng (D).
Vậy đường thẳng (D) có vô số vec-tơ chỉ phương
Trong không gian tọa độ Oxyz cho đường thẳng có phương trình x - 1 2 = y + 1 - 1 = z 2 và mặt phẳng α có phương trình x+y-z-2=0. Tính côsin của góc tạo bởi đường thẳng ∆ và mặt phẳng α
![]()
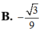
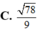
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình lần lượt d: x = 1+2t, y = 2 - t, z = 3t . Tìm tọa độ điểm K đối xứng với điểm I(2;-1;3) qua đường thẳng d
A. K(4;3;3)
B. K(1;-3;3)
C. K(-4;-3;-3)
D. K(-1;3;-3)
Chọn A
Mặt phẳng qua I vuông góc với d có phương trình
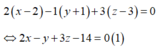
Gọi H là hình chiếu của I trên đường thẳng d.
Thay x, y, z từ phương trình của d vào (1) ta có

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình x = 1 + 2 t y = t z = 2 - t . Gọi d’là hình chiếu vuông góc của đường thẳng d trên mặt
A. u 1 → = 2 ; 0 ; 1
B. u 1 → = 1 ; 1 ; 0
C. u 1 → = - 2 ; 1 ; 0
D. u 1 → = 2 ; 1 ; 0
Trong không gian với hệ tọa độ Oxyz, cho điểm M ( 1;-3;2 ) và đường thẳng ∆ có phương trình x - 1 1 = y 2 = z - 2 1 . Tọa độ hình chiếu vuông góc của điểm M trên đường thẳng ∆ là
A. ( 0;-2;1 )
B. ( -1;1;-1 )
C. ( 1;0;2 )
D. ( 2;2;3 )
Gọi H 1 + t ; 2 t ; 2 + t ∈ ∆ là hình chiếu vuông góc của M trên đường thẳng ∆ .
Ta có M H → 1 + t ; 2 t ; 2 + t và u ∆ → 1 ; 2 ; 1 là VTCP của đường thẳng ∆
Vì
M H ⊥ ∆ ⇔ M H → . u ∆ → = 0 ⇔ t + 2 2 t + 3 + t = 0 ⇔ 6 t + 6 = 0 ⇔ t = - 1
nên H ( 0;-2;1 )
Chọn đáp án A
Trong không gian Oxyz, cho đường thẳng ∆ có phương trình chính tắc x + 1 - 3 = y - 2 2 = z + 1 1 . Tọa độ một vectơ chỉ phương của ∆ là:
A. 3 ; - 2 ; - 1
B. - 3 ; 2 ; 0
C. - 1 ; 2 ; - 1
D. 1 ; - 1 ; 1
Trong không gian Oxyz, cho đường thẳng ∆ có phương trình chính tắc x + 1 - 3 = y - 2 2 = z + 1 1 . Tọa độ một vectơ chỉ phương của ∆ là:
![]()
![]()
![]()
![]()