Tính diện tích hình phẳng (phần được tô đậm) như hình vẽ dưới đây
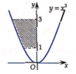
A. S = 2 3 − 2 3
B. S = 28 3
C. S = 29 3
D. S = 3 2 − 1 3
Tính diện tích hình phẳng (phần được tô đậm) như hình vẽ dưới đây
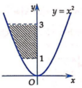
A. S = 2 3 − 2 3
B. S = 28 3
C. S = 29 3
D. S = 3 2 − 1 3
Tính diện tích hình phẳng (phần được tô đậm) như hình vẽ dưới đây
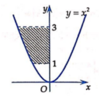

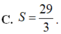
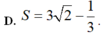
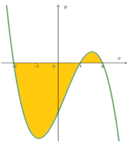
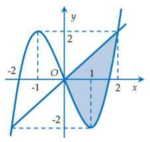
Cho đồ thị y=f(x) như hình vẽ sau đây. Biết rằng ∫ - 2 1 f ( x ) d x = a và ∫ 1 2 f ( x ) d x = b . Tính diện tích S của phần hình phẳng được tô đậm.
![]()
![]()
![]()
![]()
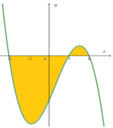
Cho đồ thị y=f(x) như hình vẽ sau đây. Biết rằng ∫ - 2 1 f ( x ) d x = a và ∫ 1 2 f ( x ) d x = b . Tính diện tích S của phần hình phẳng được tô đậm
A. S=b-a
B. S=-a-b
C. S=a-b
D. S=a+b
Chọn đáp án A
Phương pháp
Sử dụng công thức tính diện tích mặt phẳng giới hạn bởi đồ thị hàm số y=f(x), trục Ox và hai đường thẳng x=a,x=b là
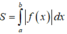
Chú ý đến dấu của f(x) khi phá dấu giá trị tuyệt đối. Nếu đồ thị nằm dưới Ox thì f(x)<0, nếu đồ thị nằm trên Ox thì f(x)>0.
Cách giải
Trên (-2;1) thì đồ thị nằm phía dưới Ox nên f(x)<0, trên khoảng (1;2) thì đồ thị nằm trên Ox nên f(x)>0
Nên từ hình vẽ ta có diện tích phần được tô đậm là
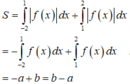
Cho đồ thị hàm số y = f(x) . Diện tích S của hình phẳng (phần tô đen trong hình vẽ) được tính theo công thức dưới đây?
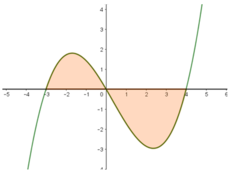

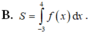
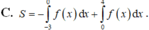
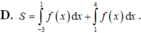
Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên. Công thức tính S là
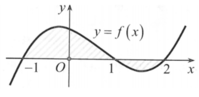
A. S = ∫ - 1 1 f x d x + ∫ 1 2 f x d x
B. S = ∫ - 1 1 f x d x - ∫ 1 2 f x d x
C. S = ∫ - 1 2 f x d x
D. S = - ∫ - 1 2 f x d x
Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên. Công thức tính S là

A. S = ∫ − 1 1 f x d x + ∫ 1 2 f x d x
B. S = ∫ − 1 1 f x d x − ∫ 1 2 f x d x
C. S = ∫ − 1 2 f x d x
D. S = − ∫ − 1 2 f x d x
Đáp án B
Dựa vào hình vẽ ta có S = ∫ − 1 1 f x d x − ∫ 1 2 f x d x
Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên. Công thức tính S là
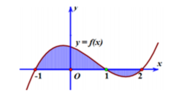
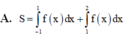
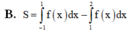
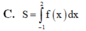
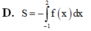
Trên mặt phẳng tọa độ Oxy, cho phần hình phẳng được tô đậm như hình bên được giới hạn bởi một đồ thị hàm số bậc ba đa thức và một đường thẳng. Diện tích S của phần tô đậm đó bằng bao nhiêu?
A. S = 8
B. S = 6
C. S = 2
D. S = 4