Biết F(x) là một nguyên hàm của f(x) và f(x) xác định trên [a;b]. Khi đó tích phân ∫ a b f ( x ) d x được tính theo công thức nào sau đây?
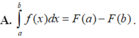
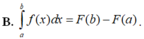
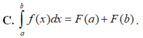
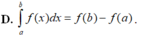
Biết F(x) là một nguyên hàm của f(x) và f(x) xác định trên [a,b]. Khi đó tích phân ∫ a b f x d x được tính theo công thức nào sau đây?
A. ∫ a b f x d x = F a − F b .
B. ∫ a b f x d x = f b − f a .
C. ∫ a b f x d x = f b − f a .
D. ∫ a b f x d x = f b − f a .
Biết F(x) là một nguyên hàm của f(x) và f(x) xác định trên [a;b]. Khi đó tích phân ∫ a b f ( x ) d x được tính theo công thức nào sau đây?
A. ∫ a b f ( x ) d x = F ( a ) − F ( b )
B. ∫ a b f ( x ) d x = F ( b ) − F ( a )
C. ∫ a b f ( x ) d x = F ( a ) + F ( b )
D. ∫ a b f ( x ) d x = f ( b ) − f ( a )
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) xác định trên K. Mệnh đề nào dưới đây sai?
A. x ∫ f x d x ' = f ' x
B. ∫ f x d x ' = f x
C. ∫ f x d x ' = F ' x
D. ∫ f x d x = F x + C
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) xác định trên K. Mệnh đề nào dưới đây sai?
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.
Cho hàm số f(x) liên tục trên [a;b] và F(x) là một nguyên hàm của f(x). Tìm khẳng định sai.
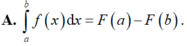
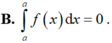
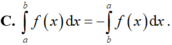
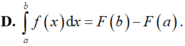
Chọn A
Định nghĩa và tính chất của tích phân.
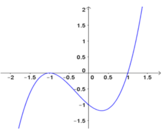
Cho hàm số y = f(x) xác định và liên tục trên khoảng K và có đạo hàm là f’(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f’(x) trên K.
Sổ điểm cực trị của hàm số f(x) trên K là
A. 2
B. 1
C. 3
D. 0
Đáp án B
Từ hình vẽ ta thấy, hàm số f'(x) = 0 có 2 nghiệm phân biệt x = 1 và x = -1.9x
Trong đó chỉ có tại x = 1 thì f'(x) đổi dấu từ âm sang dương, do đó hàm số y = f(x) có một điểm cực trị.
Cho hàm số f(x) liên tục trên đoạn [a;b] và F(x) là một nguyên hàm của f(x). Tìm khẳng định sai trong các khẳng định sau?
A. ∫ a b f x d x = F a - F b
B. ∫ a b f x d x = 0
C. ∫ a b f x d x = - ∫ a b f x d x
D. ∫ a b f x d x = F b - F a
Cho hàm số y=f(x) xác định và liên tục trên R, có đạo hàm f’(x). Biết rằng đồ thị hàm số f’(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)=f(x) +x .
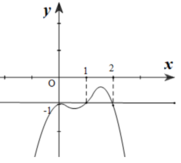
A. Không có giá trị
B. x = 0
C. x = 1
D. x = 2