Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, AB = a , AC = 2 a , SA = 3 a . Tính thể tích của khối chóp S.ABC.
A. 3 a 3
B. 2 a 3
C. 1 2 a 3
D. a 3
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, AB=a. AC=2a. SA=3a. Tính thể tích của khối chóp S.ABC.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, A B = a , A C = 2 a , S A = 3 a . Tính thể tích của khối chóp S.ABC.
A. 2 a 3
B. 2 a 3
C. 1 2 a 3
D. a 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Tính thể tích hình chóp S.AB′C′.
A. a 3 2
B. a 3 6
C. a 3 24
D. a 3 12
Cho hình chóp S.ABC có SA vuông góc với đáy, S A = a 3 , A B = a , B C = 2 a , A C = a 5 . Tính thể tích khối chóp S.ABC theo a.
A. 2 a 3 3
B. 2 a 3 3 3
C. a 3 3
D. a 3 3
Chọn B.
Phương pháp
Tính diện tích đáy và chiều cao rồi áp dụng công thức V = 1 3 S h tính thể tích.
Cách giải:
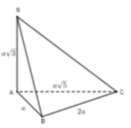

Cho hình chóp S.ABC có SA vuông góc với đáy, S A = a 3 , A B = a , B C = 2 a , A C = a 5 . Tính thể tích khối chóp S.ABC theo a.
![]()
![]()
Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB =a, AC=2a, SA vuông góc với đáy và SA =3a. Thể tích khối chóp S.ABC bằng
A. 6 a 3
B. a 3
C. 3 a 3
D. 2 a 3
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=a, AB=a, AC=2a. B A C ^ = 60 ∘ . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC.
A. V = 20 5 π a 3 3
B. V = 5 6 π a 3
C. 5 5 π 2 a 3
D. V = 5 5 6 π a 3
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=a, AB=a, AC=2a, BAC= 60 o . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC
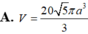
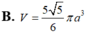
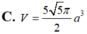
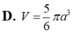
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), S A = a , A B = a , A C = 2 a , B A C = 60 ° . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC
A. V = 20 5 π a 3 3
B. V = 5 5 6 π a 3
C. V = 5 5 π 2 a 3
D. V = 5 6 π a 3
Đáp án B
Phương pháp:
- Chứng minh Δ A B C vuông tại B, tìm tâm và bán kính đường tròn ngoại tiếp tam giác đáy.
- Sử dụng công thức R 2 = h 2 4 + r 2 với R là bán kính hình cầu ngoại tiếp khối chóp, h là chiều cao, r là bán kính đường tròn ngoại tiếp đa giác đáy.
Cách giải:
Ta có: cos 60 ° = 1 2 = a 2 a → cos B A C = A B A C
⇒ Δ A B C vuông tại B.
Gọi M là trung điểm AC.
⇒ M là tâm đường tròn ngoại tiếp Δ A B C
⇒ M A = M A = A C 2 = a

Gọi r là bán kính đường tròn ngoại tiếp tam giác đáy.
R là bán kính mặt cầu ngoại tiếp hình chóp.
h là chiều cao hình chóp.
Ta có công thức sau:
R 2 = h 2 4 + r 2 ⇒ R 2 = a 2 4 + a 2 = a 5 2
⇒ V = 4 3 π R 3 = 5 a 5 6
Chú ý khi giải:
HS cần linh hoạt trong việc chứng minh Δ A B C vuông tại B và biết sử dụng công thức liên hệ giữa R, r, h.