Có bao nhiêu mặt phẳng song song với mặt phẳng ( α ) : x + y + z = 0 đồng thời tiếp xúc với mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 2 y - 2 z = 0
A. 1.
B. 0.
C. Vô số.
D. 2.
Có bao nhiêu mặt phẳng song song với mặt phẳng α : x + y + z = 0 đồng thời tiếp xúc với mặt cầu S : x 2 + y 2 + z 2 - 2 x - 2 y - 2 z = 0 ?
A. 1
B. 0
C. Vô số
D. 2
Trong không gian Oxyz cho mặt cầu (S) x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 2 = 0 và mặt phẳng α 4 x + 3 y - 12 z + 10 = 0 . Lập phương trình mặt phẳng β thỏa mãn đồng thời các điều kiện: Tiếp xúc với (S), song song với α và cắt trục Oz ở điểm có cao độ dương
A. 4 x + 3 y - 12 z - 78 = 0
B. 4 x + 3 y - 12 z - 26 = 0
C. 4 x + 3 y - 12 z + 78 = 0
D. 4 x + 3 y - 12 z + 26 = 0
Ta có:
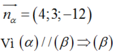
nhận n α → 4 ; 3 ; - 12 làm VTPT.
![]()
Ta có: (S) có tâm I 1 ; 2 ; 3 và bán kính
![]()
Mặt phẳng β tiếp xúc với mặt cầu
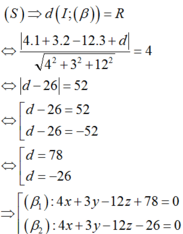
Gọi M 0 ; 0 ; z 0 z 0 > 0 là giao điểm của Oz và các mặt phẳng β 1 ; β 2
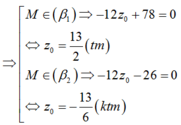
Chọn C.
Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu S : x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 ,mặt phẳng ( α ) : x + 4 y + z - 11 = 0 .Gọi (P) là mặt phẳng vuông góc với α , (P) song song với giá của véctơ v → = 1 ; 6 ; 2 và (P) tiếp xúc với (S). Lập phương trình mặt phẳng (P)
A. 2x - y + 2z - 2 = 0 và x - 2y + z - 21 = 0.
B. x - 2y + 2z + 3 = 0 và x - 2y + z - 21 = 0.
C. 2x - y + 2z + 3 = 0 và 2x - y + 2z - 21 = 0.
D. 2x - y + 2z + 5 = 0 và 2x - y + 2z - 2 = 0.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 mặt phẳng ( α ) : x + 4 y + z - 11 = 0 . Gọi (P) là mặt phẳng vuông góc với ( α ) , (P) song song với giá của vecto v → = ( 1 ; 6 ; 2 ) và (P) tiếp xúc với (S). Lập phương trình mặt phẳng ( P ).
A. 2x -y +2z -2 = 0 và x - 2y + z -21 = 0
B. x- 2y+ 2z + 3 = 0 và x - 2y + z -21 = 0
C. 2x -y +2z + 3 = 0 và 2x - y + 2z -21 = 0
D. 2x -y +2z + 5 = 0 và x - 2y + 2z -2 = 0
Đáp án C
Ta có:
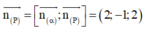
![]()
Mặt cầu (S) có tâm I(1;-3;2); R =4
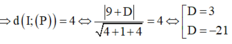
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình: x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 . Viết phương trình mặt phẳng (P) song song với giá của véc tơ v ⇀ = 1 ; 6 ; 2 , vuông góc với mặt phẳng ( α ) : x + 4 y + z - 11 = 0 và tiếp xúc với (S).

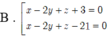
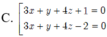
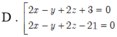
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình: x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 . Viết phương trình mặt phẳng (P) song song với giá của véc tơ v ⇀ = 1 ; 6 ; 2 , vuông góc với mặt phẳng ( α ) : x + 4 y + z - 11 = 0 và tiếp xúc với (S).
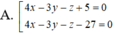
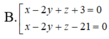

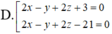
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 3
B. 7 2
C. 21 2
D. 3 2
Đáp án B
Phương pháp:
![]()
![]()
![]()
thay tọa độ điểm B vào phương trình ( α ) => 1 phương trình 2 ẩn a, b.
![]()
Sử dụng công thức tính khoảng cách
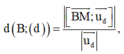
lập được 1 phương trình 2 ẩn chứa a, b.
+) Giải hệ phương trình tìm a,b => Toạ độ điểm B => Độ dài AB.
Dế thấy
![]()
Ta có
![]()
![]()
![]()
Lại có
![]()
Đường thẳng d đi qua M(0;0;-1), có u → = ( 1 ; 2 ; 2 )
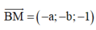
![]()
Do đó
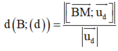
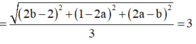
![]()
![]()
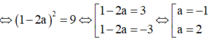
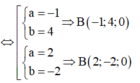
Vậy AB = 7 2
Trong không gian với hệ tọa độ Oxyz viết phương trình mặt phẳng tiếp xúc với mặt cầu x - 1 2 + y 2 + z + 2 2 = 6 đồng thời song song với hai đường thẳng d 1 : x - 2 3 = y - 1 - 1 = z - 1 ; d 2 : x 1 = y + 2 1 = z - 2 - 1 .
A. [ x - y + 2 z - 3 = 0 x - y + 2 z + 9 = 0
B. [ x + y + 2 z - 3 = 0 x + y + 2 z + 9 = 0
C. x + y + 2 z + 9 = 0
D. x - y + 2 z + 9 = 0
Ta có: (S) có tâm I 1 , 0 , - 2 và bán kính R = 6 .
d 1 có VTCP là: u 1 → 3 , - 1 , - 1
d 2 có VTCP là: u 2 → 1 , 1 , - 1
Ta có:
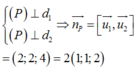
Khi đó ta có phương trình (P) có dạng:
x + y + 2 z + d = 0
Mặt phẳng (p) tiếp xúc với mặt cầu
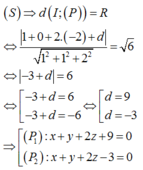
Chọn B.
Trong không gian Oxyz, cho mặt phẳng α : 2 x + y - 2 z - 2 = 0 , đường thẳng d : x + 1 2 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng α , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 2
B. 21 2
C. 7 3
D. 3 2
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 2 x + 6 y − 4 z − 2 = 0 , mặt phẳng α : x + 4 y + z − 11 = 0. Gọi (P) là mặt phẳng vuông góc với α , P song song với giá của vecto v → 1 ; 6 ; 2 v à P tiếp xúc với (S). Lập phương trình mặt phẳng ( P ).
A. 2 x − y + 2 z − 2 = 0 và x − 2 y + z − 21 = 0
B. x − 2 y + 2 z + 3 = 0 và x − 2 y + z − 21 = 0
C. 2 x − y + 2 z + 3 = 0 và 2 x − y + 2 z − 21 = 0
D. 2 x − y + 2 z + 5 = 0 và x − 2 y + 2 z − 2 = 0