Trong không gian tọa độ Oxyz, cho hai điểm A ( 1 ; 0 ; 0 ) , B ( 5 ; 6 ; 0 ) và M là điểm thay đổi trên mặt cầu S : x 2 + y 2 + z 2 = 1 . Tập hợp các điểm M trên mặt cầu (S) thỏa mãn 3 M A 2 + M B 2 = 48 có bao nhiêu phần tử?
A. 0
B. 1
C. 2
D. 3
Trong không gian với hệ tọa độ Oxyz cho hai điểm A - 1 ; - 1 ; 0 , B 3 ; 1 ; - 1 . Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:
A. M 0 ; 9 2 ; 0
B. M 0 ; 9 4 ; 0
C. M 0 ; - 9 4 ; 0
D. M 0 ; - 9 2 ; 0
Trong không gian hệ tọa độ Oxyz, cho hai điểm A ( 1 ; 2 ; - 1 ) , B vectơ A B → 1 ; 3 ; 1 . Xác định tọa độ B
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ O x y z , cho hai điểm A ( 1 ; 1 ; - 1 ) , B ( 2 ; 3 ; 2 ) . Vectơ A B → có tọa độ là
A. ( 1 ; 2 ; 3 )
B. ( - 1 ; - 2 ; 3 )
C. ( 3 ; 5 ; 1 )
D. ( 3 ; 4 ; 1 )
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(-1;-1;0), B(3;1;-1). Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:

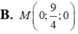
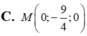

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A - 1 ; - 4 ; 2 , B 1 ; 0 ; 2 . Trung điểm M của đoạn thẳng AB có tọa độ là
A. M(2;4;0)
B. M(1;2;0)
C. M(0;-1;1)
D. M(0;-2;2)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-3;2;-1), B(1;0;5). Tọa độ trung điểm I của đoạn thẳng AB là
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, cho hai điểm A(1;-1;0) và B(1;2;-3). Tọa độ điểm M nằm trên trục Oz và cách đều hai điểm A, B là
A. M(0;0;-3)
B. M(0;0;-1)
C. M(0;0;-2)
D. M(0;0;2)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A ( 1 ; - 1 ; 2 ) và B ( 2 ; 1 ; - 4 ) . Véctơ A B → có tọa độ là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;3;-1) và B(-4;1;9). Tọa độ của véc tơ A B → là
A. (-6;-2;10)
B. (-1;2;4)
C. (6;2;-10)
D. (1;-2;-4)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;3; - 1) và B( - 4;1;9). Tọa độ của véc tơ A B → là
A. ( - 6; - 2;10)
B. ( - 1;2;4)
C. (6;2; - 10)
D. (1; - 2; - 4)