Trong không gian với hệ tọa độ Oxyz, cho véc tơ u → = ( 1 ; 1 ; - 2 ) , v → = ( 1 ; 0 ; m ) . Tìm tất c giá trị của m để góc giữa u → , v → bằng 45 ° .
![]()
![]()
![]()
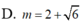
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ ![]() =(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ
=(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ![]() ?
?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho u → = ( - 2 ; 3 ; 0 ) ; v → = ( 2 ; - 2 ; 1 ) , tọa độ của véc tơ w → = u → - 2 v → là
A. (-6;7;-2)
B. (6;-8;1)
C. (6;3;0)
D. (-6;3;0)
Đáp án A
Ta có: w → = u → - 2 v → = - 2 ; 3 ; 0 - 2 2 ; - 2 ; 1 = - 6 ; 7 ; - 2
Trong không gian với hệ tọa độ Oxyz giả sử u → = 2 i → + 3 j → - k → , khi đó tọa độ véc tơ u → là
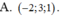
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho u → = - 2 ; 3 ; 0 , v → = 2 ; - 2 ; 1 , độ dài của véc tơ w → = u → + 2 v → là
A. 3
B. 5
C. 2
D. 9
Đáp án A
Ta có: w → = u → + 2 v → = - 2 ; 3 ; 0 + 2 2 ; - 1 ; 1 = 2 ; - 1 ; 2 . Do đó w → = 4 + 1 + 4 = 3 .
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ ![]()
A. x+2
B. 3x-2
C. 3x+2
D.-2-x
Trong không gian với hệ tọa độ Oxyz cho hai véc tơ a → = 3 ; 0 ; 2 , c → = 1 ; − 1 ; 0 . Tìm tọa độ của véc tơ b → thỏa mãn biểu thức 2 b → − a → + 4 c → = 0 →
A. 1 2 ; − 2 ; − 1
B. − 1 2 ; 2 ; 1
C. − 1 2 ; − 2 ; 1
D. − 1 2 ; 2 ; − 1
Đáp án B
Ta có a → − 4 c → = − 1 ; 4 ; 2
⇒ 2 b → = a → − 4 c → ⇒ b → = − 1 2 ; 2 ; 1
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 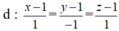 . Véc-tơ nào trong các véc-tơ sau đây không là véc-tơ chỉ phương của đường thẳng d?
. Véc-tơ nào trong các véc-tơ sau đây không là véc-tơ chỉ phương của đường thẳng d?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ ![]()
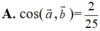
![]()
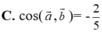
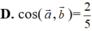
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ ![]() . Tìm tọa độ điểm A.
. Tìm tọa độ điểm A.
A. A(-2;3;0)
B. A(-2;0;3)
C. A(0;2;-3)
D. A(0;-2;3).
Trong không gian với hệ tọa độ Oxyz, cho hai véc tơ a → = ( 1 ; 0 ; - 1 ) ; b → = ( 2 ; 1 ; 1 ) . Véc tơ nào sau đây vuông góc với cả a → , b →
A. (1;0;0)
B. (0;1;0)
C. (1;3;-1)
D. (1;3;1)