Trong mặt phẳng tọa độ, điểm M - 3 ; 2 là điểm biểu diễn của số phức nào dưới đây?
A. z = 3 + 2 i
B. z = - 3 + 2 i
C. z = - 3 - 2 i
D. z = 3 - 2 i
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3 x + 2 y + z + 14 = 0
B. 2 x + y + 3 z + 9 = 0
C. 3 x + 2 y + z - 14 = 0
D. 2 x + y + z - 9 = 0
Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.
Trong mặt phẳng tọa độ Oxy phép vị tự H(1;2) tỉ số k = -3 điểm M(4;7) biến thành điểm M’ có tọa độ
A. M'(-13;-8)
B. M'(8;13)
C. M'(-8;-13)
D. M'(-8;13)
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ điểm M’ đối xứng với điểm M qua điểm P là:
A. M’(18; 10)
B. M’(18; –10)
C. M'(9/2; 1/2)
D. M’(9; – 7)
Do điểm M’ đối xứng với điểm M qua điểm P nên P là trung điểm MM’.
Suy ra:
x P = x M + x M ' 2 y P = y M + y M ' 2 ⇔ x M ' = 2 x P − x M = 2.9 − 0 = 18 y M ' = 2 y P − y M = 2. ( − 3 ) − 4 = − 10 ⇒ M ' ( 18 ; − 10 )
Đáp án B
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14=0
B. 2x+y+3z+9=0
C. 3x+2y+z-14=0
D. 2x+y+z-9=0.
Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
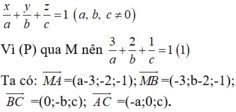
Vì M là trực tâm của tam giác ABC nên:
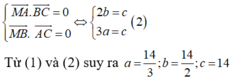
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.
Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -3, biến điểm M(-4;3) thành điểm M’ có tọa độ
A. M'(-12;-9)
B. M'(12;9)
C. M'(-9;12)
D. M'(12;-9)
O M ' → = - 3 O M →
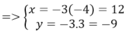
⇒ M'(12; -9)
Đáp án D
Trong không gian với hệ tọa độ Oxyz cho điểm M(1;4;2) và mặt phẳng ( α ) : x + y + z - 1 = 0 . Tọa độ điểm M’ đối xứng với điểm M qua mặt phẳng (α) là
A. M’(0;-2;-3)
B. M’(-3;-2;0)
C. M’(-2;0;-3)
D. M’(-3;0;-2)
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: A = T v → ( M )
Giả sử A = (x; y). Khi đó

Vậy A = (5; 1)
Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;2) tỉ số k = 5, biến điểm M(2;-3) thành điểm M’ có tọa độ:
A. M'(1;-5)
B.M'(8;13)
C. M'(6;-23)
D.M'(6;-27)
Phép vị tự tâm I(1; 2) tỉ số k = 5 biến điểm M(2; -3) thành điểm M’(x; y)
⇔ I M ' → = 5 I M → ⇔ x − 1 = 5 2 − 1 y − 2 = 5 − 3 − 2 ⇔ x = 6 y = − 23
Suy ra M’(6; -23).
Đáp án C
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: M = T v → ( A )
Giả sử A = (x; y). Khi đó

Vậy A = (1; 3)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(0;1;2), B(2;-2;1), C(-2;0;1) và mặt phẳng ( P ) : 2 x + 2 y + z - 3 = 0 . Tọa độ điểm M thuộc mặt phẳng (P) sao cho M cách đều ba điểm A, B, C là
A. M(-7;3;2)
B. M(2;3;-7)
C. M(3;2;-7)
D. M(3;-7;2)
Chọn B
Đặt M(x;y;z). Lập hệ 3 phương trình ba ẩn x,y,z từ phương trình mặt phẳng (P) và điều kiện MA=MB, MA=MC