Cho hàm số y = f x liên tục trên ℝ và có đạo hàm f ' x = 2 - x 2 x - 1 3 3 - x . Hàm số đồng biến trên khoảng nào dưới đây?
A. 3 ; + ∞
B. - ∞ ; 1
C. - ∞ ; 2
D. 1 ; 2
Chọn D.
Hàm số y = f x có f ' x ≥ 0 ; ∀ x ∈ K (dấu = xảy ra tại hữu hạn điểm) thì hàm số đồng biến trên khoảng K.
Ta xét
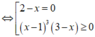
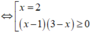
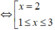
Suy ra hàm số đồng biến trên (1;3) nghĩa là hàm số đồng biến trên khoảng (1; 2)
Cho hàm số y = f x liên tục trên ℝ và có đạo hàm f ' x = 2 - x 2 x - 1 3 3 - x . Hàm số y = f x đồng biến trên khoảng nào dưới đây?
A. 3 ; + ∞
B. - ∞ ; 1
C. - ∞ ; 2
D. ( 1;2)
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. 1 ; + ∞
B. - 1 ; 0
C. - ∞ ; 1
D. 0 ; 1
Trong các hàm số dưới đây, hàm số nào không nghịch biến trên ℝ ?
A. y = - x 3 + 2 x 2 - 7 x
B. y = - 4 x + cos x
C. y = - 1 x 2 + 1
D. y = 2 2 + 3 x
Đáp án C.
Xét y = - 1 x 2 + 1 ⇒ y ' = 2 x x 2 + 1 2 → y ' = 0 ⇔ x = 0
Hàm số này đồng biến trên 0 ; + ∞ và nghịch biến trên - ∞ ; 0
Trong các hàm số sau đây, hàm số nào đồng biến trên ℝ?
A. y = x 4 - x 2
B. y = x 3 + 2 x + 2
C. y=lnx.
D. y = x - 4 x + 1
Xét phương án B, ta có y ' = 3 x 2 + 2 > 0 , ∀ x ∈ ℝ nên ta chọn B
Đáp án B
Cho hàm số y = f x liên tục trên ℝ và có đạo hàm f ' x = x + 1 2 x − 1 3 2 − x . Hàm số y = f x đồng biến trên khoảng nào dưới đây?
A. (1;2)
B. − ∞ ; − 1
C. (-1;1)
D. 2 ; + ∞
Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực ℝ ?
A. y = log 1 2 x
B. y = π 3 x
C. y = 2 e x
D. log π 4 2 x 2 + 1
Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực ℝ ?
A. y = π 3 x
B. y = log 1 2 x
C. y = log π 4 2 x 2 + 1
D. y = 2 e x
Cho hàm số y = f(x) có đạo hàm trên ℝ , thỏa mãn f − 1 = f 3 = 0 và đồ thị của hàm số y = f ' x có dạng như hình dưới đây.
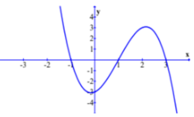
Hàm số y = f x 2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (1;2)
B. (-2;1)
C. (0;4)
D. (-2;2)
