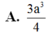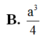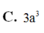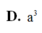Cho lăng trụ ABC.A'B'C'; M, N lần lượt là trung điểm A'B' và A’C’. Gọi V1, V2 là thể tích của hai phần lăng trụ bị chia ra bởi mặt phẳng (BCNM). Tính tỉ số V 1 V 2
A. V 1 V 2 = 5 7
B. V 1 V 2 = 3 4
C. V 1 V 2 = 1
D. V 1 V 2 = 1 2
PB
Những câu hỏi liên quan
Cho hình lăng trụ tam giác đều ABC.ABC cạnh đáy bằng a. Biết rằng bán kính mặt cầu ngoại tiếp lăng trụ ABC.ABC bằng a. Tính thể tích V của khối lăng trụ ABC.ABC A.
a
3
2
3
B.
a
3
3
3
C.
a...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' cạnh đáy bằng a. Biết rằng bán kính mặt cầu ngoại tiếp lăng trụ ABC.A'B'C' bằng a. Tính thể tích V của khối lăng trụ ABC.A'B'C'
A. a 3 2 3
B. a 3 3 3
C. a 3 3 2
D. a 3 2 2
Cho hình lăng trụ đều ABC.ABC có
A
B
2
a
;
A
A
a
3
.
. Tính thể tích khối lăng trụ ABC.ABC. A.
a
3
4
B.
3
a
3
C.
3
a
3
4
D.
a...
Đọc tiếp
Cho hình lăng trụ đều ABC.A'B'C' có A B = 2 a ; A A ' = a 3 . . Tính thể tích khối lăng trụ ABC.A'B'C'.
A. a 3 4
B. 3 a 3
C. 3 a 3 4
D. a 3
Đáp án B
Phương pháp: VABC.A'B'C' = AA'.SABC
Cách giải:
ABC.A'B'C' là lăng trụ đều ⇒ ΔABC đều
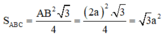
Thể tích ABC.A'B'C':
Đúng 0
Bình luận (0)
Cho lăng trụ đứng ABC.ABC có tất cả các cạnh bằng a. Thể tích khối lăng trụ ABC.ABC là A.
3
12
a
2
B.
a
3
C.
3
4
a...
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có tất cả các cạnh bằng a. Thể tích khối lăng trụ ABC.A'B'C' là
A. 3 12 a 2
B. a 3
C. 3 4 a 2
D. 2 a 3
Đáp án C
Ta có V = a . a 3 2 4 = a 3 3 4
Đúng 0
Bình luận (0)
Cho lăng trụ đứng ABC.ABC có tất cả các cạnh bằng a. Thể tích khối lăng trụ ABC.ABC là A.
3
12
a
3
B.
a
3
C.
3
4
a
3
D.
2
a
3
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có tất cả các cạnh bằng a. Thể tích khối lăng trụ ABC.A'B'C' là
A. 3 12 a 3
B. a 3
C. 3 4 a 3
D. 2 a 3
Cho lăng trụ đứng ABC.A'B'C' có tất cả các cạnh bằng a . Thể tích khối lăng trụ ABC.A'B'C' là.
Cho hình lăng trụ tam giác đều
A
B
C
.
A
B
C
có
A
B
2
a
,
A
A
a
3
. Thể tích khối lăng trụ
A
B
C
.
A
B
C
bằng A.
3
a...
Đọc tiếp
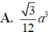
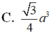
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có A B = 2 a , A A ' = a 3 . Thể tích khối lăng trụ A B C . A ' B ' C ' bằng
A. 3 a 3 4
B. a 3 4
C. 3 a 3
D. a 3
Cho hình lăng trụ tam giác đều ABC.ABC có AB2a,AA
a
3
. Tính thể tích khối lăng trụ ABC.ABC A. c B.
1
4
a
3
C.
3
a
3
D.
a
3
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB=2a,AA'= a 3 . Tính thể tích khối lăng trụ ABC.A'B'C'
A. c
B. 1 4 a 3
C. 3 a 3
D. a 3
Cho lăng trụ tam giác đều ABC.ABC có tất cả các cạnh bằng 2a. Tính thể tích khối lăng trụ ABC.ABC A.
a
3
3
B.
a
3
3
4
C.
a
3
3
2...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 2a. Tính thể tích khối lăng trụ ABC.A'B'C'
A. a 3 3
B. a 3 3 4
C. a 3 3 2
D. 2 a 3 3
Cho lăng trụ tam giác đều ABC.ABC có tất cả các cạnh bằng 2a. Tính thể tích khối lăng trụ ABC.ABC.
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 2a. Tính thể tích khối lăng trụ ABC.A'B'C'.
Cho hình lăng trụ tam giác đều ABC.ABC có AB2a, AAa
3
. Tính thể tích khối lăng trụ ABC.ABC.
Đọc tiếp
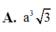
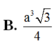
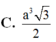
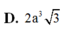
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB=2a, AA'=a 3 . Tính thể tích khối lăng trụ ABC.A'B'C'.
