Biết rằng, tập hợp các điểm biểu diễn số thức z thỏa mãn z - 2 = 6 - z + 2 là elip x 2 a 2 + y 2 b 2 = 1 . Tổng a 2 + b 2 bằng
A.. 41
B. 13
C. 5
D. 14
Tập hợp các điểm biểu diễn số thức z thỏa mãn |z+2| = |z-i| là một đường thẳng có phương trình
A. 4x + 2y + 3 = 0
B. 2x + 4y + 13 = 0
C. 2x - 4y + 13 = 0
D. x = 4 + t y = - 2 + t z = 1 + t
Trên mặt phẳng Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z - 2 + z + 2 = 6 là

B. Đường thẳng y = 6.
![]()
D. Đường tròn tâm (0;2), bán kính bằng 6
Trên mặt phẳng Oxyz tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z - 2 + z + 2 = 6 là
A. E l í p x 2 9 + y 2 5 = 1
B. Đ ư ờ n g t h ẳ n g y = 6
C. ( 0 ; 2 ) , ( 0 ; - 2 )
D. Đ ư ờ n g t r ò n t â m ( 0 ; 2 ) b á n k í n h b ằ n g 6
Cho số phức z thỏa mãn z - 2 = 2 . Biết rằng tập hợp các điểm biểu diễn các số phức w = ( 1 - i ) z + i là một đường tròn. Tính bán kính r của đường tròn đó
A. 2 2
B. 4
C. 2
D. 2
Xét các số phức z thỏa mãn ( z + 2 i ) ( z ¯ + 2 ) là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
![]()
![]()
![]()
![]()
Cho các số phức z thỏa mãn z + 1 = 2 . Biết rằng tập hợp các điểm biểu diễn các số phức w = ( 1 + i 8 ) z + i là một đường tròn. Bán kính r của đường tròn đó là
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn |z+i| = 1. Biết rằng tập hợp các điểm biểu diễn các số phức w = z - 2i là một đường tròn. Tâm của đường tròn đó là:
A. I(0;-1)
B. I(0;-3)
C. I(0;3)
D. I(0;1)
Đáp án B.
Ta có ![]()
Gọi ![]() Suy ra z = x + (2+y).i
Suy ra z = x + (2+y).i
Suy ra
Theo giả thiết, ta có ![]()
![]()
![]()
Vậy tập hợp các số phức w = z - 2i là đường tròn tâm I(0;-3).
Cho số phức z thỏa mãn z + i = 1 . Biết rằng tập hợp các điểm biểu diễn các số phức w = z − 2 i là một đường tròn. Tâm của đường tròn đó là:
A. I(0;-1)
B. I(0;-3)
C. I(0;3)
D. I(0;1)
Đáp án B.
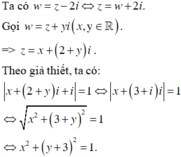
Vậy tập hợp các số phức w = z - 2i là đường tròn tâm I(0;-3).
Cho số phức z thỏa mãn |z|=2. Biết rằng tập hợp các điểm biểu diễn số phức w=3-2i+(2-i)z là một đường tròn. Tìm tọa độ tâm I của đường tròn đó?
A.I(3;-2)
B. I(-3;2)
C.I(3;2)
D.I(-3;-2)