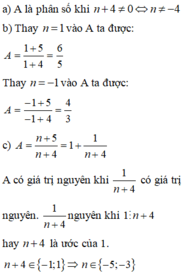Cho phân số M = n + 1 n (n ∈ ℤ ; n ≠ 0). Tìm n để A là phân số tối giản
PB
Những câu hỏi liên quan
Cho
A
n
+
5
n
+
4
với
n
∈
ℤ
.a) Tìm điều kiện của số nguyên n để A là phân số.b) Tính giá trị của của phân số A khi n 1; n -1 c) Tìm số nguyên n để phân số A có giá trị là số nguyên.
Đọc tiếp
Cho A = n + 5 n + 4 với n ∈ ℤ .
a) Tìm điều kiện của số nguyên n để A là phân số.
b) Tính giá trị của của phân số A khi n = 1; n = -1
c) Tìm số nguyên n để phân số A có giá trị là số nguyên.
có thể có phân số \(\frac{a}{b}\)(a,b thuộc \(ℤ\), b \(\ne\)0 ) sao cho :
\(\frac{a}{b}=\frac{a.m}{b.n}\)(m ,n thuộc\(ℤ\); m ,n khác 0 và m không bằng n) hay không ?
không thể, vì để có phân số mới bằng phân số a/b thì m=n và n khác 0
Đúng 0
Bình luận (0)
có nhưng chỉ với a=0
còn a khác thì ko đc!
Đúng 0
Bình luận (0)
có thể có phân số a/b (a,b thuộc \(ℤ\), b \(\ne\)0 ) sao cho :
a/b =a.m/b.n (m ,n thuộc\(ℤ\); m ,n khác 0 và m không bằng n) hay không ?
có phân số a/b (a;b thuộc Z, b khác 0) và a/b = am/bn khi a = 0
VD :
0/b = 0.m/bn
Đúng 0
Bình luận (0)
\(\frac{a}{b}=\frac{a}{b}.\frac{m}{n}\Leftrightarrow\frac{a}{b}\left(1-\frac{m}{n}\right)=0\Leftrightarrow\orbr{\begin{cases}\frac{a}{b}=0\\\frac{m}{n}=1\end{cases}}\)
Do \(m\ne n\Rightarrow\frac{m}{n}\ne1\Rightarrow\frac{a}{b}=0\Rightarrow a=0\)
Vậy a=0, b là số nguyên khác 0
Đúng 0
Bình luận (0)
Cho tích phân
I
∫
1
2
3
d
x
x
+
1
2
x
+
3
. Đặt
t
2
x
+
3...
Đọc tiếp
Cho tích phân I = ∫ 1 2 3 d x x + 1 2 x + 3 . Đặt t = 2 x + 3 ta được I = ∫ 2 3 m t 2 + n d t (với m , n ∈ ℤ ). Tính T = 3m + n
A. T = 7.
B. T = 2.
C. T = 4.
D. T = 5.
Chọn D.
Tính I = ∫ 1 2 3 d x x + 1 2 x + 3
Đặt t = 2 x + 3 ⇒ t 2 = 2 x + 3 ⇒ 2 t d t = 2 d x x = t 2 - 3 2 ⇒ d x = t d t x + 1 = t 2 - 1 2
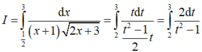
Vậy: m = 2, n = -1, T = 3.2 - 1 = 5.
Đúng 0
Bình luận (0)
Cho phân số B = 10 n 5 n − 3 ( n ∈ ℤ )
a) Tìm n để B có giá trị nguyên.
b) Tìm giá trị lớn nhất của B.
a) B = 10 n 5 n − 3 = 10 n − 6 5 n − 3 + 6 5 n − 3 = 2. 5 n − 3 5 n − 3 + 6 5 n − 3 = 2 + 6 5 n − 3
B có giá trị nguyên khi 6 5 n − 3 có giá trị nguyên, tức là 6 ⋮ 5 n − 3 hay 5 n − 3 ∈ Ư ( 6 ) .
Ư ( 6 ) = ± 1 ; ± 2 ; ± 3 ; ± 6
Ta có bảng sau:
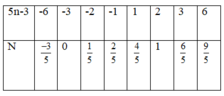
Dựa vào bảng ta thấy n ∈ 0 ; 1
b) B đạt giá trị lớn nhất khi 6 5 n − 3 đạt giá trị lớn nhất, tức là 5n-3 đạt giá trị nguyên dương nhỏ nhất, khi n=1. Khi đó GTLN của B là 5.
Đúng 0
Bình luận (0)
Tìm n ∈ ℤ sao cho:
6n + 35 là bội số của n + 3
Đáp số n ∈ { ................ }
Dùng dấu chấm phảy (;) hoặc dấu phảy (,) để phân cách các số
Tìm n ∈ ℤ sao cho:
8n + 1 là bội số của n + 2
Đáp số n ∈ { }
Dùng dấu chấm phảy (;) hoặc dấu phảy (,) để phân cách các số
Ta có 8n+1=8(n+2)-8
=> 8 chia hết cho n+2
n nguyên => n+2 nguyên => n+2 \(\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
Ta có bảng
| n+2 | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| n | -10 | -6 | -4 | -3 | -1 | 0 | 2 | 6 |
Cho hai tập hợp
M
{
8
k
+
5
|
k
∈
ℤ
}
,
N
{
4
l
+
1
|
l
∈
ℤ
}
.Khẳng định nào sau đây là đúng? A.
M
⊂
N
B.
N
⊂
M
C.
M
N
D.
M
∅
,
N
∅
Đọc tiếp
Cho hai tập hợp M = { 8 k + 5 | k ∈ ℤ } , N = { 4 l + 1 | l ∈ ℤ } .
Khẳng định nào sau đây là đúng?
A. M ⊂ N
B. N ⊂ M
C. M = N
D. M = ∅ , N = ∅
Tìm n ∈ ℤ sao cho:
n + 9 là ước số của 4n + 22
Đáp số n ∈ { }
Dùng dấu chấm phảy (;) hoặc dấu phảy (,) để phân cách các số
Ta có: n + 9 là ước số của 4n + 22
=> 4n + 22 chia hết n + 9
<=> (4n + 36) - 14 chia hết n + 9
<=> 4.(n + 9) - 14 chia hết n + 9
=> 14 chia hết n + 9
=> n + 9 \(\in\) Ư(14) = { - 1;1;-2;2;-3;3;-4;4;-7;7-14;14}
=> n= { tự tính hộ nhé}
Đúng 0
Bình luận (0)
Ta có: n + 9 là ước số của 4n + 22
=> 4n + 22 chia hết n + 9
<=> (4n + 36) - 14 chia hết n + 9
<=> 4.(n + 9) - 14 chia hết n + 9
=> 14 chia hết n + 9
=> n + 9 $\in$∈ Ư(14) = { - 1;1;-2;2;-3;3;-4;4;-7;7-14;14}
=> n= { tự tính hộ nhé}
Đúng 0
Bình luận (0)
Ta có: n + 9 là ước số của 4n + 22
=> 4n + 22 chia hết n + 9
<=> (4n + 36) - 14 chia hết n + 9
<=> 4.(n + 9) - 14 chia hết n + 9
=> 14 chia hết n + 9
=> n + 9 $\in$∈ Ư(14) = { - 1;1;-2;2;-3;3;-4;4;-7;7-14;14}
=> n= { tự tính hộ nhé}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời