Giá trị lớn nhất của hàm số y = x - 2 + 4 - x là
A. 2 2
B. 4
C. 2
D. 2
Gọi M mà m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = 1 - x - 2 x 2 x + 1 . Khi đó giá trị của M-m là:
A. -2
B. -1
C. 1
D. 2
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6) x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.
A. 4
B. -2
C. -22
D. 5
Chọn A
Hàm số f(x) = (x-6) x 2 + 4 xác định và liên tục trên đoạn [0;3].
![]()
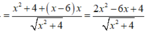

![]()
Suy ra ![]()
![]()
![]() với a là số nguyên và b, c là các số nguyên dương nên
với a là số nguyên và b, c là các số nguyên dương nên
a = - 12, b = 3, c = 13. Do đó: S = a + b + c = 4.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 x - 4 6 - x trên đoạn [-3;6]. Tổng M + m có giá trị là
A. 18
B. -6
C. -12
D. -4
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) = x 3 - 3 x 2 trên đoạn [-1;1]. Tính M + m.
A. -4
B. 4
C. -2
D. 2
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = xlnx trên đoạn 1 2 e ; e lần lượt là
A. M = e , m = - 1 2 e ln 2 e
B. M = e , m = - 1 2 e
C. M = - 1 2 e ln 2 e , m = - e - 1
D. M = e , m = - 1 e
Cho hàm số f(x) liên tục trên đoạn [0;3] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên [0;3]. Giá trị của M + m bằng ?
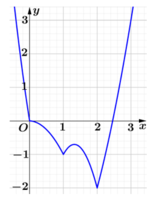
A. 5
B. 3
C. 2
D. 1
Chọn D
Dựa vào hình vẽ ta có : M = 3, m = -2. Do đó: M + m = 1
GIá trị lớn nhất của hàm số:
\(P=\sqrt[4]{1-x^2}+\sqrt[4]{1-x}+\sqrt[4]{1+x}\)
Lời giải:
Đặt $\sqrt[3]{1-x}=a; \sqrt[4]{1+x}=b$ thì bài toán trở thành:
Cho $a,b\geq 0$ thỏa mãn $a^4+b^4=2$
Tìm max $P=ab+a+b$
Thật vậy, áp dụng BĐT AM-GM:
$2=a^4+b^4\geq 2a^2b^2\Rightarrow ab\leq 1$
$a^4+b^4\geq \frac{1}{2}(a^2+b^2)^2$
$a^2+b^2\geq \frac{1}{2}(a+b)^2$
$\Rightarrow 2=a^4+b^4\geq \frac{(a+b)^4}{8}$
$\Rightarrow (a+b)^4\leq 16$
$\Rightarrow a+b\leq 2$
Do đó: $P=ab+a+b\leq 1+2=3$
Vậy $P_{\max}=3$ khi $a=b=1\Leftrightarrow x=0$
Giá trị lớn nhất của hàm số y = 2 x - 1 x 2 trên khoảng - ∞ ; 0 là
A. -1.
B. 0.
C. -2.
D. -3.
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = $\sqrt{\sin x}+\sqrt{1-\sin x}$ \(\left(0\le x\le\dfrac{\pi}{2}\right)\). Tính M4-m4
Áp dụng BĐT \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\):
\(y^2=\left(\sqrt{sinx}+\sqrt{1-sinx}\right)^2\le sinx+1-sinx=1\)
\(\Rightarrow-1\le y\le1\)
\(\Rightarrow M^4-m^4=0\)